题目内容
4.阅读材料:如图1,△ABC的周长为l,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.∵S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=$\frac{1}{2}$AB•r,S△OBC=$\frac{1}{2}$BC•r,S△OCA=$\frac{1}{2}$CA•r
∴S△ABC=$\frac{1}{2}$AB•r+$\frac{1}{2}$BC•r+$\frac{1}{2}$CA•r=$\frac{1}{2}$l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图2)且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
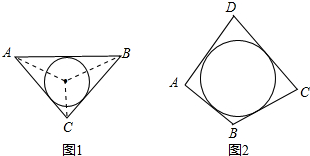
分析 (1)根据上述三角形的内切圆的半径公式,由已知条件,结合勾股定理的逆定理得该三角形是直角三角形.可以首先求得其面积与周长,再根据其公式代入计算;
(2)同样连接圆心和四边形的各个顶点以及圆心和各切点,根据四边形的面积等于四个三角形的面积进行计算;
(3)根据上述方法和结论,即可猜想到:任意多边形的内切圆的半径等于其面积的2倍除以多边形的周长.
解答 解:(1)∵5,12,13为边长的三角形为直角三角形,
∴ S=$\frac{1}{2}$×5×12=30,周长l=5+12+13=30,
S=$\frac{1}{2}$×5×12=30,周长l=5+12+13=30,
∵S=$\frac{1}{2}$l•r,
∴30=$\frac{1}{2}$×30×r,
解得:r=2;
(2)连接OA,OB,OC,OD,并设内接圆半径为r,
∵S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA=$\frac{1}{2}$a•r+$\frac{1}{2}$b•r+$\frac{1}{2}$c•r+$\frac{1}{2}$d•r=$\frac{1}{2}$(a+b+c+d)•r.
∴r=$\frac{2S}{a+b+c+d}$;
(3)猜想:r=$\frac{2S}{{a}_{1}+{a}_{2}+…+{a}_{n}}$.
点评 此题属于圆的综合题.考查了内切圆的性质、勾股定理的逆定理以及三角形面积问题.注意把n边形分成n个三角形进行计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某多边形的内角和是其外角和的4倍,则此多边形的边数是( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
16.下列命题中,原命题与其逆命题均为真命题的是( )
| A. | 同位角相等 | B. | 全等三角形的对应角相等 | ||
| C. | 若a=b,则|a|=|b| | D. | 等腰三角形的两底角相等 |
14.近三年来,我县职业中专的基础设施建设大幅度提升,实调设备购置累计资金1005.69万元,总值达到了2009万元,在校生规模达到3240余人.9个专业中,6个专业达到了规范化专业标准,将3240用科学记数法表示为( )
| A. | 324×101 | B. | 3.24×104 | C. | 3.24×103 | D. | 32.4×102 |

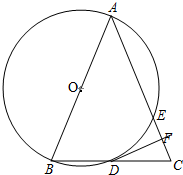 如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证:
如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证: