题目内容
1.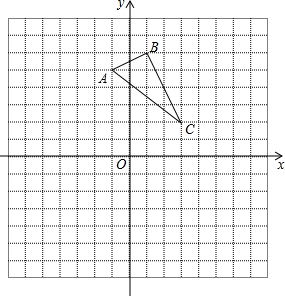 已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.
已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.
分析 利用轴对称性质,作出A、B、C关于x轴的对称点,A1、B1、C1,顺次连接A1B1、B1C1、C1A1,即得到关于x轴对称的△A1B1C1.
解答 解:如图所示: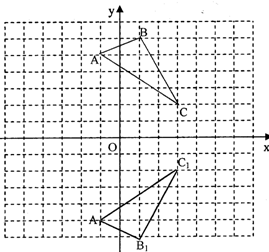
点评 本题考查了轴对称作图,作轴对称后的图形的依据是轴对称的性质,基本作法是:
①先确定图形的关键点;
②利用轴对称性质作出关键点的对称点;
③按原图形中的方式顺次连接对称点.

练习册系列答案
相关题目
9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
16.下列命题中,原命题与其逆命题均为真命题的是( )
| A. | 同位角相等 | B. | 全等三角形的对应角相等 | ||
| C. | 若a=b,则|a|=|b| | D. | 等腰三角形的两底角相等 |
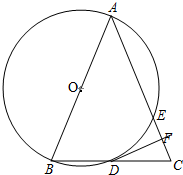 如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证:
如图,AB为⊙O的直径,点D为⊙O上的一点,在BD的延长线上取点C,使DC=BD,AC与⊙O交于点E,DF⊥AC于点F.求证: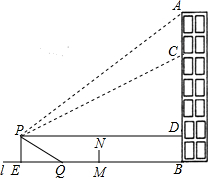 如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.