题目内容
8.拼图与数学:(1)如图1,观察左边方格图中阴影所示的图形(注:每一小方格的边长为1).若将它剪开,可重新拼成一个正方形,请你在右边的方格图中画出你所拼成的正方形,可用阴影增加效果,并写出你所拼成的正方形的边长$\sqrt{5}$;
(2)如图2是用4个相同的小长方形与1个正方形镶嵌而成的正方形图案.若用x、y表示小长方形的两边长(x>y),则请利用图中的面积关系直接写来代数式x+y、x-y、xy三者之间存在着等式关系:(x+y)2-4xy=(x-y)2;
(3)如图3,右图是2002年在北京召开的国际数学家大会的会标,它来源于我国古代著名的“赵爽弦图”.它是由4个全等的直角三角形(如左图,三边长分别为BC=a、AC=b、AB=c)及中间一个小正方形拼成的大正方形.请你利用图中的面积关系推导出一个有关直角三角形三边长a、b、c简洁的等量关系.
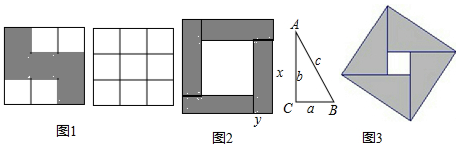
分析 (1)根据正方形的面积求出边长,即可得解;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式x+y、x-y、xy之间的等量关系.
(3)先表示出中间小正方形的边长,然后根据大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积列出等式,然后整理即可得解.
解答 解:(1)如图1所示: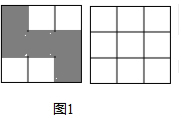
(2)代数式x+y、x-y、xy三者之间存在着等式关系:(x+y)2-4xy=(x-y)2;
(3)它能说明的等式为:c2=a2+b2.
推导如下:中间小正方形的边长为(b-a),
∴大正方形的面积可表示为:
c2=4×$\frac{1}{2}$ab+(b-a)2,
整理得,c2=2ab+b2-2ab+a2,
即c2=a2+b2.
故答案为:$\sqrt{5}$;(x+y)2-4xy=(x-y)2.
点评 本题考查了图形的剪拼,主要利用了正方形的面积,勾股定理,根据面积求出边长,再利用勾股定理作出相应边长的正方形即可,灵活掌握并运用网格结构是解题的关键.

练习册系列答案
相关题目
13.用火柴棒按下列方式搭建三角形:

(1)填表:
(2)当有n个三角形时,应用多少根火柴棒?(用含n的代数式表示);
(3)当有2015根火柴棒时,照这样可以摆多少个三角形?

(1)填表:
| 三角形个数 | 1 | 2 | 3 | 4 |
| 火柴棒根数 | 3 | 5 | 7 | 9 |
(3)当有2015根火柴棒时,照这样可以摆多少个三角形?
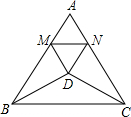 如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5.
如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为5.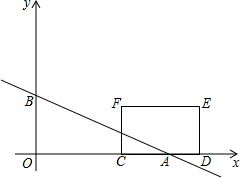 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{3}$x+b(b>0),分别交x轴、y轴于A、B两点,点C(3,0),D(6,0),以CD为一边在x轴上方作矩形CDEF,CF=$\sqrt{3}$,设矩形CDEF与△ABO重叠部分的面积为S.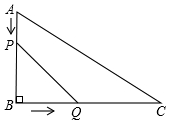 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问:
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问: