��Ŀ����
3���Ķ����ϣ������κ��������ǹ涨����$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$��������$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc�����磺$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1��4-2��3=-2��
��1����������涨���������$|\begin{array}{l}{1}&{-2}\\{3}&{-1}\end{array}|$|��ֵ��
��2����������涨��������� ��x-2��2+��y+$\frac{1}{5}$��2=0ʱ��$|\begin{array}{l}{-3{x}^{2}+y}&{{x}^{2}+y}\\{3}&{-2}\end{array}|$ֵ��
���� ��1�����������֪�г�ʽ����⣮
��2���Ȼ��������ʽ�ӣ�Ȼ��x��y��ֵ���뼴������𰸣�
��� �⣺��1���������֪��$|\begin{array}{l}{1}&{-2}\\{3}&{-1}\end{array}|$=1����-1��-��-2����3=-1+6=5��
��2���ߣ�x-2��2+��y+$\frac{1}{5}$��2=0��
��x=2��y=-$\frac{1}{5}$��
��$|\begin{array}{l}{-3{x}^{2}+y}&{{x}^{2}+y}\\{3}&{-2}\end{array}|$=-2��-3x2+y��-3��x2+y��
=6x2-2y-3x2-3y
=3x2-5y
=3��4-5����-$\frac{1}{5}$��
=12+1
=13
���� ���⿼���¶��������㣬�漰��ʽ�ļӼ����������������ģ���Ŀ��Ϊ�ۺϣ�

��ϰ��ϵ�д�
 53���ò�ϵ�д�
53���ò�ϵ�д�
�����Ŀ
18����֪xy��0����xy=y-x�����ʽ$\frac{1}{x}$-$\frac{1}{y}$��ֵΪ��������
| A�� | xy | B�� | y-x | C�� | 1 | D�� | -1 |
12��������ͼ����ʾ�ķ�����ͼ�Σ�

��1��������
��2���������εĸ�����15ʱ�������ĸ����ж��٣�
��3���������εĸ�����nʱ�������ĸ�����α�ʾ��

��1��������
| �����εĸ��� | 1 | 2 | 3 | 4 | �� |
| �����ĸ��� | 3 | 5 | 7 | 9 | �� |
��3���������εĸ�����nʱ�������ĸ�����α�ʾ��
 ��ͼ����֪E��F��������ABCD�ı�BC��CD�ϵ����㣬��AE=AF����ô����AB=4ʱ����AEF�����S��CE�ij�x�ĺ���������ǣ�д�����ı���ʽ�����ش�xȡ��ֵʱ����AEF����������ģ������ʱ��AEF�������������ABCD�����֮�ȣ�
��ͼ����֪E��F��������ABCD�ı�BC��CD�ϵ����㣬��AE=AF����ô����AB=4ʱ����AEF�����S��CE�ij�x�ĺ���������ǣ�д�����ı���ʽ�����ش�xȡ��ֵʱ����AEF����������ģ������ʱ��AEF�������������ABCD�����֮�ȣ�
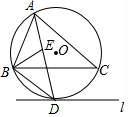 ��ͼ����O�ǡ�ABC�����Բ��ֱ��l���O�����ڵ�D����l��BC��
��ͼ����O�ǡ�ABC�����Բ��ֱ��l���O�����ڵ�D����l��BC��