题目内容
20.已知$\frac{x}{y}$=$\frac{2}{7}$,求$\frac{{x}^{2}-3xy+2{y}^{2}}{2{x}^{2}-3xy+7{y}^{2}}$的值.分析 设比例系数的方法,由$\frac{x}{y}$=$\frac{2}{7}$可设x=2t,y=7t,再把它们代入原式进行整式的运算,然后约分即可.
解答 解:∵$\frac{x}{y}$=$\frac{2}{7}$,
∴设x=2t,y=7t,
∴$\frac{{x}^{2}-3xy+2{y}^{2}}{2{x}^{2}-3xy+7{y}^{2}}$=$\frac{4{t}^{2}-3×14{t}^{2}+2×49{t}^{2}}{2×4{t}^{2}-3×14{t}^{2}+7×49{t}^{2}}$=$\frac{20}{103}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式

练习册系列答案
相关题目
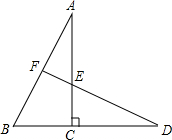 如图所示,已知:AB•EC=BC•DE.试说明:
如图所示,已知:AB•EC=BC•DE.试说明: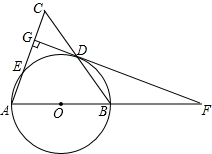 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.