题目内容
11.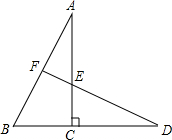 如图所示,已知:AB•EC=BC•DE.试说明:
如图所示,已知:AB•EC=BC•DE.试说明:(1)DF⊥AB;
(2)EF•DF=BF•AF.
分析 (1)由AB•EC=BC•DE,得到$\frac{AB}{DE}=\frac{BC}{CE}$,由于∠ACB=∠DCE=90°,推出△ABC∽△DCE,于是得到∠D=∠A,结论即可得出;
(2)根据∠A=∠D,∠AFE=∠DFB,得到△AFE∽△DFB,即可得到结论.
解答 证明: ∵AB•EC=BC•DE,
∵AB•EC=BC•DE,
∴$\frac{AB}{DE}=\frac{BC}{CE}$,
∵∠ACB=∠DCE=90°,
∴△ABC∽△DCE,
∴∠D=∠A,
∵∠A+∠B=90°,
∴∠D+∠B=90°,
∴∠DFB=90°,
∴DF⊥AB;
(2)∵∠A=∠D,∠AFE=∠DFB,
∴△AFE∽△DFB,
∴$\frac{EF}{BF}=\frac{AF}{DF}$,
∴EF•DF=BF•AF.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
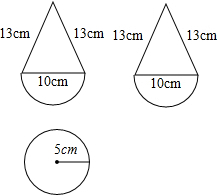 某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其容积.(球的体积公式:V=$\frac{4}{3}$πr3)
某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其容积.(球的体积公式:V=$\frac{4}{3}$πr3)