题目内容
15.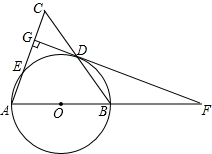 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=$\frac{2}{5}$,求CG的长.
分析 (1)首先判断出OD∥AC,推得∠ODG=∠DGC,然后根据DG⊥AC,可得∠DGC=90°,∠ODG=90°,推得OD⊥FG,即可判断出直线FG是⊙O的切线.
(2)首先根据相似三角形判定的方法,判断出△ODF∽△AGF,再根据cosA=$\frac{2}{5}$,可得cos∠DOF=$\frac{2}{5}$;然后求出OF、AF的值,即可求出AG、CG的值各是多少.
解答 (1)证明:如图1,连接OD,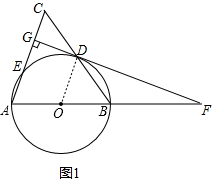
∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)解:如图2,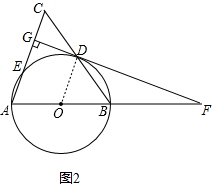
∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,
$\left\{\begin{array}{l}{∠DOF=∠A}\\{∠F=∠F}\end{array}\right.$
∴△ODF∽△AGF,
∴$\frac{OD}{AG}=\frac{OF}{AF}$,
∵cosA=$\frac{2}{5}$,
∴cos∠DOF=$\frac{2}{5}$,
∴$OF=\frac{OD}{cos∠DOF}$=$\frac{5}{\frac{2}{5}}=\frac{25}{2}$,
∴AF=AO+OF=5$+\frac{25}{2}=\frac{35}{2}$,
∴$\frac{5}{AG}=\frac{\frac{25}{2}}{\frac{35}{2}}$,
解得AG=7,
∴CG=AC-AG=10-7=3,
即CG的长是3.
点评 (1)此题主要考查了切线的判定和性质的应用,要熟练掌握,解答此题的关键是要明确切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案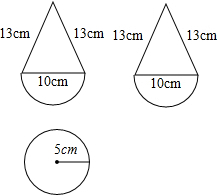 某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其容积.(球的体积公式:V=$\frac{4}{3}$πr3)
某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其容积.(球的体积公式:V=$\frac{4}{3}$πr3)