题目内容
9. 如图,AC平分∠BAD,CE⊥AB,垂足为E,∠ADC+∠B=180°,AB=10,AD=6.
如图,AC平分∠BAD,CE⊥AB,垂足为E,∠ADC+∠B=180°,AB=10,AD=6.求证:BC=CD.
分析 作CF⊥AD交AD的延长线于F,根据角平分线的性质得到CE=CF,证明Rt△BEC≌Rt△DFC,根据全等三角形的性质证明结论.
解答 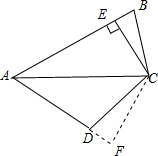 证明:作CF⊥AD交AD的延长线于F,
证明:作CF⊥AD交AD的延长线于F,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,
∵∠ADC+∠B=180°,又∠ADC+∠CDF=180°,
∴∠B=∠CDF,
在Rt△BEC和Rt△DFC中,
$\left\{\begin{array}{l}{∠B=∠CDF}\\{∠BEC=∠DFC}\\{CE=CF}\end{array}\right.$,
∴Rt△BEC≌Rt△DFC,
∴BC=CD.
点评 本题考查的是角平分线的性质和三角形全等的判定和性质,掌握角的平分线上的点到角的两边的距离相等、灵活运用三角形全等的判定定理和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,有一矩形空地,一边是长为20米的墙,另三边是由一根长34米的铁丝围成,且与墙平行的一边有一个1米宽的小门.已知矩形空地的面积是125平方米,求矩形空地的长和宽.
如图,有一矩形空地,一边是长为20米的墙,另三边是由一根长34米的铁丝围成,且与墙平行的一边有一个1米宽的小门.已知矩形空地的面积是125平方米,求矩形空地的长和宽.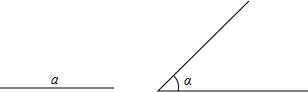 已知线段a和∠α,尺规作图:
已知线段a和∠α,尺规作图: