题目内容
19.已知关于x的方程x2-3(m+1)x+m(m+3)=0.求证:无论m取何值,此方程都有两个不相等的实数根.分析 表示出根的判别式,配方后得到根的判别式大于0,进而确定出方程总有两个不相等的实数根.
解答 证明:∵△=[-3(m+1)]2-4m(m+3)=5m2+6m+9=5(m+$\frac{3}{5}$)2+$\frac{36}{5}$,
∵(m+$\frac{3}{5}$)2≥0,
∴5(m+$\frac{3}{5}$)2+$\frac{36}{5}$>0,
∴无论m取何实数时,此方程都有两个不相等的实数根.
点评 此题考查了根的判别式,根的判别式的值大于0,方程有两个不相等的实数根;根的判别式的值等于0,方程有两个相等的实数根;根的判别式的值小于0,方程没有实数根.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.下列运算中,结果正确的是( )
| A. | (-22)3=-6a6 | B. | a3•a2=a5 | C. | a4+a4=a8 | D. | (a-b)2=a2-b2 |
 如图,宽为50cm的矩形图案由10个全等的小长方形拼成,设小长方形的长为xcm,宽为ycm,则下列方程组$\left\{\begin{array}{l}2x=x+4y\\ x+y=50\end{array}\right.$,$\left\{\begin{array}{l}x=2x-4y\\ x+y=50\end{array}\right.$,$\left\{\begin{array}{l}x=4y\\ 2x({x+y})=10xy\end{array}\right.$,$\left\{\begin{array}{l}x=4y\\ 2x•50=10xy\end{array}\right.$中,能正确反映题中数量关系的有( )
如图,宽为50cm的矩形图案由10个全等的小长方形拼成,设小长方形的长为xcm,宽为ycm,则下列方程组$\left\{\begin{array}{l}2x=x+4y\\ x+y=50\end{array}\right.$,$\left\{\begin{array}{l}x=2x-4y\\ x+y=50\end{array}\right.$,$\left\{\begin{array}{l}x=4y\\ 2x({x+y})=10xy\end{array}\right.$,$\left\{\begin{array}{l}x=4y\\ 2x•50=10xy\end{array}\right.$中,能正确反映题中数量关系的有( )
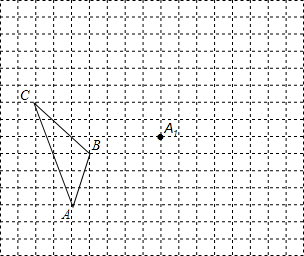 在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-4,-1).
在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(-4,-1). 如图,AC平分∠BAD,CE⊥AB,垂足为E,∠ADC+∠B=180°,AB=10,AD=6.
如图,AC平分∠BAD,CE⊥AB,垂足为E,∠ADC+∠B=180°,AB=10,AD=6.