题目内容
17.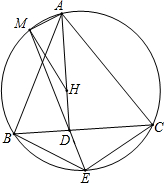 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
分析 作高BP,CQ.连结MB、MC、MP、MQ、PQ.构建相似三角形△MBQ∽△MCP,从而推知点M、A、P、Q、H五点共圆,最后根据圆周角定理证得结论.
解答 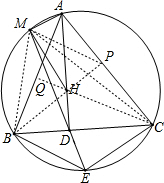 证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.
证明:作高BP,CQ.连结MB、MC、MP、MQ、PQ.
$\frac{BD}{DC}$=$\frac{{S}_{△BME}}{{S}_{△CME}}$
=$\frac{\frac{1}{2}BM•BE•sin∠MBE}{\frac{1}{2}CM•CE•sin∠MCE}$=$\frac{BM}{CM}$•$\frac{AB}{AC}$①
$\frac{BD}{DC}$=$\frac{BQ}{CP}$•$\frac{AP}{AQ}$=$\frac{BQ}{CP}$•$\frac{AB}{AC}$②
由①②得:$\frac{BM}{CM}$=$\frac{BQ}{CP}$,
又∵∠MBA=∠MCA,
∴△MBQ∽△MCP,
∴点M、A、P、Q四点共圆,即点M、A、P、Q、H五点共圆,
又AH为直径,
∴∠AMH=90°.
点评 本题考查了梅涅劳斯定理及塞瓦定理,掌握塞瓦定理与梅涅劳斯定理是解题的关键,不是初中教学内容,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在平面直角坐标系中,正方形OABC的顶点A坐标为(2,1),点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
| A. | -$\sqrt{5}$ | B. | -2 | C. | 2 | D. | $\sqrt{5}$ |
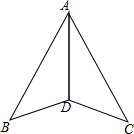 如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?
如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?
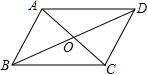 如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.
如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.