题目内容
9.根据不等式的基本性质,把下列不等式化为“x>a”或“x<a”的形式.(1)$\frac{1}{3}<\frac{1}{4}(8-x)$;
(2)-5x+6<4x-12.
分析 (1)根据性质2两边都乘以12,去分母后去括号,再根据性质1两边都加上3x,移项后合并同类项,最后根据性质2两边都除以3将系数化为1可得;
(2)根据性质1两边都减去4x,再合并同类项后依据性质3两边都除以-9将系数化为1可得.
解答 解:(1)去分母,得:4<3(8-x),
去括号,得:4<24-3x,
移项,得:3x<24-4,
合并同类项,得:3x<20,
系数化为1,得:x<$\frac{20}{3}$;
(2)移项,得:-5x-4x<-12-6,
合并同类项,得:-9x<-18,
系数化为1,得:x>2.
点评 主要考查了不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
 如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.
如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.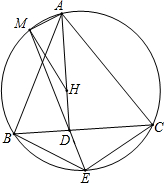 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.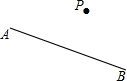 如图,以线段AB为一条对角线,直线AB外一点P为一个顶点画平行四边形.
如图,以线段AB为一条对角线,直线AB外一点P为一个顶点画平行四边形.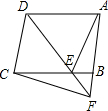 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证: