题目内容
8.在数学的学习中,我们要学会总结,不断地归纳,思考和运用,这样才能提高我们解决问题的能力,下面这个问题大家一定似曾相识:(1)比较大小:①2+3>2$\sqrt{2×3}$;②3+$\frac{1}{4}$>2$\sqrt{3×\frac{1}{4}}$;③8+8= 2$\sqrt{8×8}$;
(2)通过上面三个计算,我们可以初步对任意的非负实数a,b做出猜想:a+b≥2$\sqrt{ab}$;
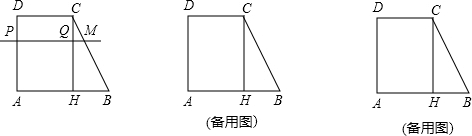
(3)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上的中线,AD=2a,DB=2b,试根据图形证明上述不等式a+b≥2$\sqrt{ab}$,并指出等号成立的条件.
(4)探索应用:如图2有一个等腰梯形工件(厚度不计),其面积为7200cm2,现在要用细包装带如图那样包扎(虚线表示包装带,四点为四边中点),则至少需要包装带的长度为240$\sqrt{2}$cm.

分析 (1)利用平方法比较大小(两个都是非负数)即可;
(2)由于a,b为非负数,利用作差法先比较它们的平方,再结合a2≥0,即可;
(3)利用射影定理,直角三角形斜边的中线等于斜边的一半;
(4)利用梯形的面积公式和前面得到的结论,即可.
解答 解:(1)①∵(2+3)2=25,(2$\sqrt{2×3}$)=4×6=24,
而25>24,
∴2+3>2$\sqrt{2×3}$,
②∵(3+$\frac{1}{4}$)2=$\frac{169}{16}$,(2$\sqrt{3×\frac{1}{4}}$)2=3,
而$\frac{169}{16}$>3,
∴3+$\frac{1}{4}$>$\sqrt{3×\frac{1}{4}}$,
③∵8+8=16,2$\sqrt{8×8}$=2×8=16,
∴8+8=2$\sqrt{8×8}$;
故答案为>,>,=;
(2)∵对任意的非负实数a,b,
∴(a+b)2-(2$\sqrt{ab}$)2=a2+b2+2ab-4ab=a2+b2-2ab=(a-b)2;
∵(a-b)2≥0,
∴(a+b)2-(2$\sqrt{ab}$)2≥0,
∴a+b≥2$\sqrt{ab}$;
(3)根据射影定理得到:CD2=AD×BD,
∵AD=2a,BD=2b,
∴CD2=4ab,
∴CD=2$\sqrt{ab}$,
∵CO是Rt△ABC斜边上的中线,
∴OC=$\frac{1}{2}$(AD+BD)=$\frac{1}{2}$(2a+2b)=a+b,
Ⅰ、当直角三角形不为等腰直角三角形时,
∵OC是Rt△OCD斜边,
∴OC>CD,
∴a+b>2$\sqrt{ab}$
Ⅱ、当直角三角形是等腰直角三角形时,点C,D重合,
∴OC=CD,
∴a+b=2$\sqrt{ab}$
即:OC≥CD,
∴a+b≥2$\sqrt{ab}$;
故答案为a+b≥2$\sqrt{ab}$(当a=b时,取等号);
(4)设EG=a,FH=b,
根据梯形面积公式得,ab=7200,
∵a+b≥2$\sqrt{ab}$=2$\sqrt{7200}$=120$\sqrt{2}$,
∴a+b的最小值为60$\sqrt{2}$,
∴包装带至少需要2(a+b)=2×120$\sqrt{2}$=240$\sqrt{2}$cm.
点评 此题是四边形综合题,主要考查了比较无理数大小的一种方法(针对两个非负数,平方大的它也大),射影定理,直角三角形斜边的中线等于斜边的一半,用平方法比较无理数大小的方法是解本题的关键,用几何图形证明结论是本题的难点.

| A. | 1.239×10-3 | B. | 1.2×10-3 | C. | 1.239×10-2 | D. | 1.239×10-4 |
 已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根,k为正整数. 如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.
如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.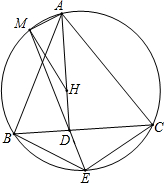 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.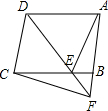 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证: