��Ŀ����
12�������з��̺ͷ����飮��1��$\frac{\sqrt{2}}{\sqrt{2}-1}$x+$\frac{1}{\sqrt{2}+1}$=2x+1
��2��$\left\{\begin{array}{l}{\sqrt{2}x-\sqrt{3}y=\sqrt{2}+\sqrt{3}}\\{\sqrt{3}x-\sqrt{2}y=\sqrt{2}-\sqrt{3}}\end{array}\right.$��
���� ��1���Ƚ���ĸ���������ٽⷽ�̼��ɽ���⣻
��2�����ݼӼ���Ԫ���ⷽ���鼴�ɽ���⣮
��� �⣺��1��$\frac{\sqrt{2}}{\sqrt{2}-1}$x+$\frac{1}{\sqrt{2}+1}$=2x+1
��ĸ����������
$\sqrt{2}��\sqrt{2}+1��x+\sqrt{2}-1=2x-1$
ȥ���ţ���
$2x+\sqrt{2}x+\sqrt{2}-1=2x-1$
����ϲ�ͬ�����
$\sqrt{2}x=-\sqrt{2}$
��ã�x=-1��
��2��$\left\{\begin{array}{l}{\sqrt{2}x-\sqrt{3}y=\sqrt{2}+\sqrt{3}}&{��}\\{\sqrt{3}x-\sqrt{2}y=\sqrt{2}-\sqrt{3}}&{��}\end{array}\right.$
$�١�\sqrt{2}-�ڡ�\sqrt{3}$����
x=-5
��x=-5����٣���
y=-2$\sqrt{6}$-1
��ԭ������Ľ���$\left\{\begin{array}{l}{x=-5}\\{y=-2\sqrt{6}-1}\end{array}\right.$��
���� ���⿼����θ�ʽ��Ӧ�ã�����Ĺؼ�����ȷ�ⷽ�̵ķ��������ĸ��������

��ϰ��ϵ�д�
 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
�����Ŀ
2��ʹ����ʽx-2��-3��2x+3��5ͬʱ������x������ֵ�ǣ�������
| A�� | -2��-1��0 | B�� | 0��1 | C�� | -1��0 | D�� | ������ |
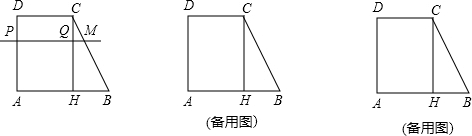
 ��ͼ��ƽ���ı���ABCD���ܳ�Ϊ60���ף�BF��DE�ֱ�Ϊ�ߣ�DC�ij�Ϊ18���ף�
��ͼ��ƽ���ı���ABCD���ܳ�Ϊ60���ף�BF��DE�ֱ�Ϊ�ߣ�DC�ij�Ϊ18���ף�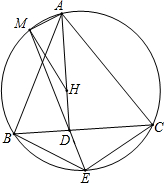 ��ͼ����ABC�Ĵ���ΪH��AD��BC��D����E�ڡ�ABC�����Բ�ϣ�������$\frac{BE}{CE}=\frac{AB}{AC}$��ֱ��ED�����Բ�ڵ�M����֤����AMH=90�㣮
��ͼ����ABC�Ĵ���ΪH��AD��BC��D����E�ڡ�ABC�����Բ�ϣ�������$\frac{BE}{CE}=\frac{AB}{AC}$��ֱ��ED�����Բ�ڵ�M����֤����AMH=90�㣮