题目内容
7.用代入消元法解二元一次方程组:(1)$\left\{\begin{array}{l}{2x+3y=3}\\{x+2y=1}\end{array}\right.$ (2)$\left\{\begin{array}{l}{2a+3b+1=0}\\{3a+2b+4=0}\end{array}\right.$ (3)$\left\{\begin{array}{l}{9x-7y-12=0}\\{3y=2+x}\end{array}\right.$ (4)$\left\{\begin{array}{l}{\frac{x}{2}=\frac{y}{3}}\\{3x+4y=18}\end{array}\right.$.
分析 各方程组利用代入消元法求出解即可.
解答 解:(1)将方程组$\left\{\begin{array}{l}{2x+3y=3}&{①}\\{x+2y=1}&{②}\end{array}\right.$,
由②得:x=1-2y ③,
将③代入①,得:2(1-2y)+3y=3,解得:y=-1,
将y=-1代入③,得:x=5,
故方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$;
(2)解方程组$\left\{\begin{array}{l}{2a+3b+1=0}&{①}\\{3a+2b+4=0}&{②}\end{array}\right.$,
由②得:a=$\frac{1-3b}{2}$ ③,
将③代入②,得:$\frac{3(1-3b)}{2}$+2b+4=0,
解得:b=$\frac{11}{5}$,
将b=$\frac{11}{5}$代入③,得:a=-$\frac{14}{5}$,
故方程组的解为:$\left\{\begin{array}{l}{a=-\frac{14}{5}}\\{b=\frac{11}{5}}\end{array}\right.$;
(3)解方程组$\left\{\begin{array}{l}{9x-7y-12=0}&{①}\\{3y=2+x}&{②}\end{array}\right.$,
由②得:x=3y-2 ③,
将③代入①,得:9(3y-2)-7y-12=0,
解得:y=$\frac{3}{2}$,
将y=$\frac{3}{2}$代入③,得:x=$\frac{5}{2}$,
故方程组的解为:$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{3}{2}}\end{array}\right.$;
(4)解方程组$\left\{\begin{array}{l}{\frac{x}{2}=\frac{y}{3}}&{①}\\{3x+4y=18}&{②}\end{array}\right.$,
由①得,3x=2y ③,
将③代入②,得:2y+4y=18,
解得:y=3,
将y=3代入③,得:3x=6,
解得:x=2,
故方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | -2,-1,0 | B. | 0,1 | C. | -1,0 | D. | 不存在 |
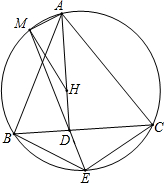 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.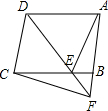 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证: