题目内容
5.如图,等腰直角△ABC腰长为10,现分别按图1、图2方式在△ABC内裁剪一个内接正方形ADFE和正方形PMNQ.设正方形ADFE的面积为S1,正方形PMNQ的面积为S2,(1)在图1 中,求AD:AB的值;在图2中,求AP:AB的值;
(2)比较S1和S2的大小,判断哪种裁剪方式所得正方形面积大.

分析 (1)图1:根据等腰三角形的性质求解;图2:同图1的求法;
(2)由(1)得出的AB、AD、AP、AB的关系,由正方形的面积公式求出S1、S2和S,即可得出结果.
解答 解:(1)图1中,∵△ABC是等腰直角三角形,四边形ADFE是正方形,
∴AD=DF,∠B=45°,
∴DF=DB,
∴AD=DB,
∴AD:AB=1:2,
图2中,同理:PM=MN,∠B=45°,
∴PM=MB,
∴MN=MB,
∴MN=MB=NC,
∴AP:AB=PQ:BC=MN:BC=1:3;
(2)S1>S2;图1的裁剪方式所得正方形面积大;理由如下:
图1中,S1=($\frac{1}{2}$×10)2=25,
∵PQ:BC=AP:AB=1:3,∴AP=AQ=$\frac{1}{3}$AB=$\frac{10}{3}$,
∴PQ=$\frac{10\sqrt{2}}{3}$,
∴S2=($\frac{10\sqrt{2}}{3}$)2=$\frac{200}{9}$<25,
∴S1>S2;
∴图1的裁剪方式所得正方形面积大.
点评 此题考查了正方形的性质、等腰直角三角形的性质、正方形面积的计算;熟练掌握正方形的性质是解决问题的关键.

练习册系列答案
相关题目
13. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)| A. | x | B. | 180°-2x | C. | 180°-x | D. | 2x |
14. 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )| A. | 2a+b | B. | 2a | C. | b | D. | -2a-b |
 将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=70°,则∠AED=55°.
将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEF=70°,则∠AED=55°. 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6.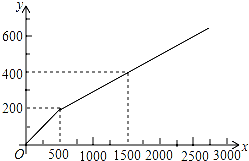 为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.
为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.