题目内容
15.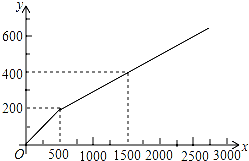 为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.
为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.(1)分别写出x<500 和x>500时,收费y与印刷页数x之间的函数关系式.
(2)当收费为180元和540元时,印刷的页数分别是多少页?
分析 (1)设当x<500时,正比例函数的解析式为y=kx(k≠0),再把x=500时,y=200代入求出k的值即可;设当x>500时,一次函数的解析式为y=ax+b(a≠0),再把当x=500时,y=200和x=1500时,y=400代入求出a、b的值即可;
(2)把y=180代入正比例函数的解析式求出x的值;分把y=540代入一次函数的解析式即可得出x的值.
解答 解:(1)当x<500时,设正比例函数的解析式为y=kx(k≠0),
∵当x=500时,y=200,
∴200=500k,解得k=$\frac{2}{5}$,
∴正比例函数的解析式为y=$\frac{2}{5}$x;
当x>500时,
设一次函数的解析式为y=ax+b(a≠0),
∵当x=500时,y=200;x=1500时,y=400,
∴$\left\{\begin{array}{l}500a+b=200\\ 1500a+b=400\end{array}\right.$,
解得a=$\frac{1}{5}$,b=100.
∴一次函数的解析式为y=$\frac{1}{5}$x+100;
(2)当y=180时,$\frac{2}{5}$x=180,解得x=450;
当y=540时,$\frac{1}{5}$x+100=540,解得x=2200.
答:当收费为180元和540元时,印刷的页数分别是450页和2200页.
点评 本题考查的是一次函数的应用,熟知利用待定系数法求一次函数的解析式是解答此题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目


 如图,按要求画图:
如图,按要求画图: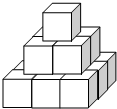 如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.
如图,把14个棱长为1cm的正方体木块,在地面上堆成如图所示的立体图形,然后向露出的表面部分喷漆,若1cm2需用漆2g,那么共需用漆84g.