题目内容
11.已知关于x的二次方程ax2+bx+c=0没有实数根,一位老师改动了方程的二项式系数后,得到的新方程有两个根为-1和$\frac{5}{3}$;另一位老师改动原来方程的某一个系数的符号,所得到的新方程的两个根为-2和10,那么$\frac{b+c}{a}$=28.分析 首先根据一位老师改动了方程的二次项系数后,得到的新方程有两个根为-1和$\frac{5}{3}$,求作一个符合条件的一元二次方程,即x2-$\frac{2}{3}$x-$\frac{5}{3}$=0,进而表示原方程是ax2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0;再根据另一位老师改动原来方程的某一个系数的符号,所得到的新方程的两个根为-2和10,求作一个符合条件的一元二次方程,即x2-8x-20=0,此方程两边同乘以$\frac{1}{12}$k,得$\frac{1}{12}$kx2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0,从而得到a=$\frac{1}{12}$k,最后即可求解.
解答 解:利用新方程有两个根为-1和$\frac{5}{3}$构造1个一元二次方程为:x2-(-1+$\frac{5}{3}$)x-1×$\frac{5}{3}$=0 即x2-$\frac{2}{3}$x-$\frac{5}{3}$=0,与ax2+bx+c=0对应.于是得到:b=-$\frac{2}{3}$k,c=-$\frac{5}{3}$k.(其中k是不为0的整数.)
从而原方程为:ax2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0.同样再由另一个新方程的两个根-2和10,构造一个方程:
x2-(-2+10)x+(-2)×10=0,
即x2-8x-20=0.
此方程两边同乘以$\frac{1}{12}$k,得 $\frac{1}{12}$kx2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0,
它与ax2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0对应,得 a=$\frac{1}{12}$k,从而原方程就是:$\frac{1}{12}$kx2-$\frac{2}{3}$kx-$\frac{5}{3}$k=0,所以$\frac{b+c}{a}$=$\frac{-\frac{2}{3}k-\frac{5}{3}k}{\frac{1}{12}k}$=28.
故答案为28.
点评 此题考查了一元二次方程根与系数的关系,能够根据已知的两根求作一个一元二次方是解题的关键.

 画如图所示物体的俯视图,正确的是( )
画如图所示物体的俯视图,正确的是( )| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{25}{x}$=$\frac{35}{x-20}$ | B. | $\frac{25}{x-20}$=$\frac{35}{x}$ | C. | $\frac{25}{x}$=$\frac{35}{x+20}$ | D. | $\frac{25}{x+20}$=$\frac{35}{x}$ |
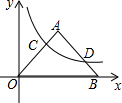 如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.
如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.
