题目内容
13. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)| A. | x | B. | 180°-2x | C. | 180°-x | D. | 2x |
分析 延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2x,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和得到∠AEB′=180°-∠B′-x,则∠C′+2x=180°-∠B′-x,所以∠C′+∠B′=180°-3x,利用三角形外角性质和等角代换得到∠BFC=∠C=x+∠C′+∠B′,所以∠BFC=180°-2x.
解答 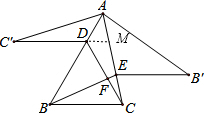 解:延长C′D交AC于M,如图,∵△ADC≌△ADC′,△AEB≌△AEB′,∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,
解:延长C′D交AC于M,如图,∵△ADC≌△ADC′,△AEB≌△AEB′,∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,
∴∠C′MC=∠C′+∠C′AM=∠C′+2x,
∵C′D∥B′E,
∴∠AEB=∠C′MC,
∵∠AEB′=180°-∠B′-∠B′AE=180°-∠B′-x,
∴∠C′+2x=180°-∠B′-x,
∴∠C′+∠B′=180°-3x,
∵∠BFC=∠BDF+∠DBF=∠DAC+∠B′=x+∠ACD+∠B′=x+∠C′+∠B′
=x+180°-3x=180°-2x.
故选B.
点评 本题考查了全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等.也考查了平行线的性质.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
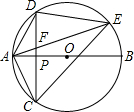 如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE.
如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE. 如图,在等边△ABC中,D,E,F分别为边AB,BC,CA上的点,且满足∠DEF=60°.
如图,在等边△ABC中,D,E,F分别为边AB,BC,CA上的点,且满足∠DEF=60°.
