题目内容
11.某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
分析 (1)根据“销售量=原销量-因价格上涨而减少的销售量”、“总利润=单件利润×销售量”可得函数解析式;
(2)求出w=8000时x的值即可得;
(3)先根据“销售单价不低于35元,且商场要完成不少于350件的销售任务”求得x的范围,再将w=-10x2+1000x-16000配方成顶点式,利用二次函数的性质求解可得.
解答 解:(1)根据题意,知:销售单价为x元时,销售量y=500-10(x-30)=-10x+800,
则销售玩具的利润w=(x-20)(-10x+800)=-10x2+1000x-16000,
完成表格如下:
| 销售单价(元) | x |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
解得:x=60或x=40,
答:该玩具销售单价x应定为40元或60元;
(3)由题意知,$\left\{\begin{array}{l}{x≥35}\\{-10x+800≥350}\end{array}\right.$,
解得:35≤x≤45,
∵w=-10x2+1000x-16000=-10(x-50)2+9000,
∴当x<50时,w随x的增大而增大,
∴当x=45时,w取得最大值,最大值为8750元.
答:商场销售该品牌玩具获得的最大利润是8750元.
点评 本题主要考查二次函数和一元二次方程的应用,解题的关键是根据题意确定解题所需的相等关系,并熟练掌握二次函数的性质.

练习册系列答案
相关题目
1.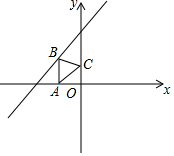 如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
 如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )| A. | $\sqrt{10}$ | B. | 2+$\sqrt{2}$ | C. | 1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{3}$ | D. | 1-$\frac{\sqrt{2}+\sqrt{5}}{2}$ |
3.下列因式分解正确的是( )
| A. | x2+9=(x+3)2 | B. | a2+4a+4=(a+2)2 | C. | a3-4a=a(a2-4) | D. | 1-4x2=(1+4x)(1-4x) |
20.下列叙述中,正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 老师测量跳远成绩的依据是两点之间,线段最短 | |
| C. | 从直线外一点到这条直线上的各点所连接的线段中,垂线段最短 | |
| D. | 一个角一定不等于它的余角 |
 某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.
某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系. 如图,在?ABCD中,AC=BC,AE⊥DC于点E,若∠B=65°,则∠CAE的度数为25°.
如图,在?ABCD中,AC=BC,AE⊥DC于点E,若∠B=65°,则∠CAE的度数为25°.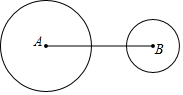 如图,⊙A、⊙B的半径分别为2、1,且AB=8,若作⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,与⊙B相交,则⊙C的半径在下列数字中可能是( )
如图,⊙A、⊙B的半径分别为2、1,且AB=8,若作⊙C使得三圆的圆心在同一直线上,且⊙C与⊙A外切,与⊙B相交,则⊙C的半径在下列数字中可能是( ) 如图,在?ABCD中,∠ABC的平分线交AD于点E,且AE=3.5,ED=2,则?ABCD的周长是18.
如图,在?ABCD中,∠ABC的平分线交AD于点E,且AE=3.5,ED=2,则?ABCD的周长是18.