题目内容
1.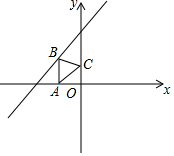 如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )
如图,已知点A(-1,0),点B是直线y=x+2上的动点,点C是y轴上的动点,则△ABC的周长的最小值等于( )| A. | $\sqrt{10}$ | B. | 2+$\sqrt{2}$ | C. | 1-$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{3}$ | D. | 1-$\frac{\sqrt{2}+\sqrt{5}}{2}$ |
分析 作点A关于直线y=x+2的对称点A′,作点A关于y轴的对称点A″,连接A′A″交直线y=x+2于B,交y轴于C,根据“两点之间,线段最短”可得出此时△ABC的周长取最小值,由点A的坐标可得出点A′、A″的坐标,利用勾股定理(或两点间的距离公式)即可求出A′A″的长度,此题得解.
解答 解:作点A关于直线y=x+2的对称点A′,作点A关于y轴的对称点A″,连接A′A″交直线y=x+2于B,交y轴于C,如图1所示.
∵点A、A′关于直线y=x+2对称,点A、A″关于y轴对称,
∴AB=A′B,AC=A″C.
∴C△ABC=AB+BC+CA=A′B+BC+CA″=A′A″(由两点之间,线段最短,可得出此时△ABC的周长最小).
过点A′作AD⊥x轴于点D,如图2所示.
∵直线的解析式为y=x+2,AA′⊥该直线,
∴∠DAA′=45°,
∴△ADA′为等腰直角三角形,点D为直线y=x+2与x轴的交点,
∴点D(-2,0),AD=1,
∴点A′(-2,1).
∵点A、A″关于y轴对称,点A(-1,0),
∴点A″(1,0).
在Rt△A′DA″中,A′D=1,A″D=1-(-2)=3,
∴A′A″=$\sqrt{A′{D}^{2}+A″{D}^{2}}$=$\sqrt{10}$.
故选A.
点评 本题考查的是一次函数图象上点的坐标特点、轴对称中的最短路线问题以及解直角三角形,找出△ABC的周长取最小值时点B、C的位置是解题的关键.

练习册系列答案
相关题目
9.已知二次函数y=x2经过两点(x1,y1),(x2,y2),当|x1|>|x2|时,y1,y2的大小关系是( )
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
16.某厂生产一种工具,据市场调查,若按每个工具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个工具的固定成本Q(元)与月销售y(个)满足如下关系:
(1)写出月产销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月销量y(个) | 100 | 160 | 240 | 320 |
| 每个工具的固定成本Q(元) | 96 | 60 | 40 | 30 |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
6.下列四个判断,其中错误的是( )
| A. | 数字0也是单项式 | B. | 单项式a的系数与次数都是1 | ||
| C. | $\frac{1}{2}$x2y2是二次单项式 | D. | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ |
10. 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )| A. | ∠B=∠B′ | B. | PA=PA′ | ||
| C. | BC=AA′ | D. | MN是线段AA′的垂直平分线 |
11.某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
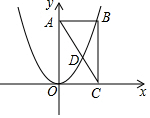 如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,抛物线y=ax2经过矩形OABC的顶点B,交对角线AC于点D.则$\frac{AD}{AC}$的值为$\frac{\sqrt{5}-1}{2}$. 如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)
如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)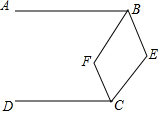 如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.
如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.