题目内容
2. 某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.
某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费y(元)与用水量x(吨)之间的函数关系.(1)当用水量≥10吨时,求y关于x的函数解析式(并写出定义域);
(2)按上述分段收费标准,小明家四、五月份分别交水费42元和27元,问五月份比四月份节约用水多少吨?
分析 (1)观察函数图象找出点的坐标,利用待定系数法即可求出当用水量≥10吨时,y关于x的函数解析式;
(2)利用待定系数法求出当0≤x≤10时,y关于x的函数解析式,再利用一次函数图象上点的坐标特征,分别求出四、五月份的用水量,二者做差后即可得出结论.
解答 解:(1)设x≥10时,y关于x的函数解析式为y=kx+b,
将点(10,30)、(20,70)代入y=kx+b,
$\left\{\begin{array}{l}{10k+b=30}\\{20k+b=70}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=4}\\{b=-10}\end{array}\right.$,
∴当用水量≥10吨时,y关于x的函数解析式为y=4x-10(x≥10).
(2)设当0≤x≤10时,y关于x的函数解析式为y=mx,
将点(10,30)代入y=mx,
30=10m,解得:m=3,
∴y=3x(0≤x≤10).
当y=4x-10=42时,x=13;
当y=3x=27时,x=9.
13-9=4(吨).
答:五月份比四月份节约用水4吨.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)利用待定系数法求出函数解析式;(2)利用一次函数图象上点的坐标特征,分别求出四、五月份的用水量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
 如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )
如图,已知△ABC和△A′B′C′关于直线MN对称,点P是直线MN上一点,连接PA、PA′、AA′,下列结论错误的是( )| A. | ∠B=∠B′ | B. | PA=PA′ | ||
| C. | BC=AA′ | D. | MN是线段AA′的垂直平分线 |
11.某商场经营某种品牌的玩具,进价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是500件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(2)在(1)问条件下,若商场获得了8000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(1)不妨设该种品牌玩具的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
| 销售单价(元) | x |
| 销售量y(件) | -10x+800 |
| 销售玩具获得利润w(元) | -10x2+1000x-16000 |
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于35元,且商场要完成不少于350件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
 如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)
如图,AB,CD相交于点O,AO=CO,试添加一个条件使得△AOD≌△COB,你添加的条件是∠A=∠C(只需填写一个)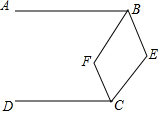 如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.
如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.