题目内容
20．下列叙述中，正确的是（ ）| A． | 相等的两个角是对顶角 | |
| B． | 老师测量跳远成绩的依据是两点之间，线段最短 | |
| C． | 从直线外一点到这条直线上的各点所连接的线段中，垂线段最短 | |
| D． | 一个角一定不等于它的余角 |
分析 根据对顶角相等；垂线段的性质：垂线段最短；余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角进行分析即可．
解答 解：A、相等的两个角是对顶角，说法错误；
B、老师测量跳远成绩的依据是两点之间，线段最短，说法错误；
C、从直线外一点到这条直线上的各点所连接的线段中，垂线段最短，说法正确；
D、一个角一定不等于它的余角，说法错误；
故选：C．
点评 此题主要考查了垂线段的性质和余角、对顶角的性质，关键是掌握垂线段最短；对顶角相等．
练习册系列答案
相关题目
10．
如图，已知△ABC和△A′B′C′关于直线MN对称，点P是直线MN上一点，连接PA、PA′、AA′，下列结论错误的是（ ）
如图，已知△ABC和△A′B′C′关于直线MN对称，点P是直线MN上一点，连接PA、PA′、AA′，下列结论错误的是（ ）| A． | ∠B=∠B′ | B． | PA=PA′ | ||
| C． | BC=AA′ | D． | MN是线段AA′的垂直平分线 |
11．某商场经营某种品牌的玩具，进价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
（2）在（1）问条件下，若商场获得了8000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
| 销售单价（元） | x |
| 销售量y（件） | -10x+800 |
| 销售玩具获得利润w（元） | -10x2+1000x-16000 |
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
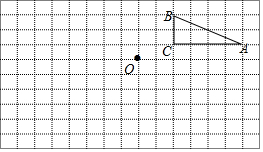如图，在边长为1个单位长度的小正方形组成的网格中，点A，B，C，O都在格点上．
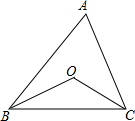如图，已知点O是△ABC的两条角平分线的交点，
9．估计$\sqrt{5}$+1的值在两个整数（ ）
| A． | 2月3之间 | B． | 3与4之间 | C． | 5与6之间 | D． | 6与7之间 |