题目内容
15．（1）先化简，再求值：（2a+b）（2a-b）+b（2a+b）-4a2，其中a=-$\frac{1}{2}$，b=2．（2）解方程组：$\left\{\begin{array}{l}{3x-2y=-6}\\{\frac{x}{2}+\frac{y}{3}=5}\end{array}\right.$．
分析 （1）先算乘法，再合并同类项，最后代入求出即可；
（2）整理后①+②即可求出x，把x的值代入①即可求出y．
解答 解：（1）（2a+b）（2a-b）+b（2a+b）-4a2
=4a2-b2+2ab+b2-4a2
=2ab，
当a=-$\frac{1}{2}$，b=2时，原式=2×（-$\frac{1}{2}$）×2=-2；
（2）整理得：$\left\{\begin{array}{l}{3x-2y=-6①}\\{3x+2y=30②}\end{array}\right.$
①+②得：6x=24，
x=4，
把x=4代入①得：12-2y=-6，
解得：y=9，
所以原方程组的解为：$\left\{\begin{array}{l}{x=4}\\{y=9}\end{array}\right.$．
点评 本题考查了整式的混合运算和求值，解二元一次方程组的应用，能正确根据整式的运算法则进行化简是解（1）的关键，能把二元一次方程组转化成一元一次方程是解（2）的关键．
练习册系列答案
相关题目
10．
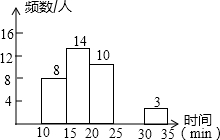某校中午学生用餐比较拥挤，为建议学校分年级错时用餐，李老师带领数学学习小组在某天随机调查了部分学生，统计了他们从下课到就餐结束所用的时间，并绘制成统计表和如图所示的不完整统计图．
根据以上提供的信息，解答下列问题：
（1）表中a=35%，b=5，c=40，补全频数分布直方图；
（2）此次调查中，中位数所在的时间段是15≤x＜20min．
（3）这所学校共有1200人，试估算从下课到就餐结束所用时间不少于20min的共有多少人？
某校中午学生用餐比较拥挤，为建议学校分年级错时用餐，李老师带领数学学习小组在某天随机调查了部分学生，统计了他们从下课到就餐结束所用的时间，并绘制成统计表和如图所示的不完整统计图．根据以上提供的信息，解答下列问题：
（1）表中a=35%，b=5，c=40，补全频数分布直方图；
（2）此次调查中，中位数所在的时间段是15≤x＜20min．
| 时间分段/min | 频（人）数 | 百分比 |
| 10≤x＜15 | 8 | 20% |
| 15≤x＜20 | 14 | a |
| 20≤x＜25 | 10 | 25% |
| 25≤x＜30 | b | 12.50% |
| 30≤x＜35 | 3 | 7.50% |
| 合计 | c | 100% |
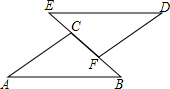如图，△ABC≌△DEF，∠A=30°，∠B=50°，BF=8．
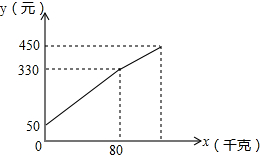李大爷按每千克2.1元批发了一批蜜橘到镇上出售，为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降低出售．售出蜜橘千克数x与他手中持有的钱数y元（含备用零钱）的关系如图所示，结合图象回答下列问题：