题目内容
7.已知函数y=x2-4x+1.(1)利用配方法求函数的对称轴,顶点坐标和最小值;
(2)设函数图象与x轴的交点为A(x1,0)、B(x2,0),求x12+x22的值.
分析 (1)加4再减4,化成完全平方,得y=(x-2)2-3,分别写出对称轴,顶点坐标和最小值;
(2)由根据与系数的关系先计算:x1+x2=4,x1x2=1,再将x12+x22进行变形为(x1+x2)2-2x1x2,代入计算即可.
解答 解:(1)∵y=x2-4x+1=x2-4x+4-4+1=(x-2)2-3,
∴当x=2时,y最小值=3,
对称轴为x=2,顶点为(2,-3);
(2)由题意,x1,x2是方程x2-4x+1=0的两根,
∴x1+x2=4,x1x2=1,
∴x12+x22=(x1+x2)2-2x1x2=42-2×1=14.
点评 本题考查了二次函数的性质和抛物线与x轴的交点问题,利用顶点式可以表示二次函数的对称轴、顶点坐标和最值:二次函数y=a(x-h)2+k中,①当a>0时,对称轴是直线x=h,顶点坐标为(h,k),因为图象有最低点,所以函数有最小值,当x=h时,y有最小值是k;②当a<0时,对称轴是直线x=h,顶点坐标为(h,k),因为图象有最高点,所以函数有最大值,当x=h时,y有最大值是k;求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;反之,知道交点坐标,可由根与系数关系计算代数式的值,如第(2)问.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
17.某公司准备用1万元从厂家购进表中的酸奶,设购进A种酸奶x箱,全部售完这批酸奶所获得利润为y元.
(1)求利润y(元)与x(箱)之间的函数关系式;
(2)如果A、B两种酸奶进货量都不超过300箱,请你设计一个可获得最大利润的进货方案,并求出最大利润.
| 进货价/(元/箱) | 出售加价率 | |
| A种酸奶 | 16 | 20% |
| B种酸奶 | 20 | 25% |
(2)如果A、B两种酸奶进货量都不超过300箱,请你设计一个可获得最大利润的进货方案,并求出最大利润.
 如图,CD是△ABC的角平分线,∠A=55°,∠B=70°,则∠1=27.5°.
如图,CD是△ABC的角平分线,∠A=55°,∠B=70°,则∠1=27.5°.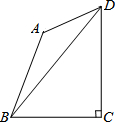 如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.
如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=4,tan∠BDC=$\frac{\sqrt{6}}{3}$.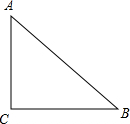 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,现有一点O从点A出发,沿AB方向运动,当到达点B时,运动停止,以点O为圆心,r为半径的圆记为⊙O.