题目内容
20.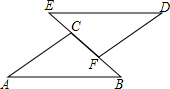 如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.(1)求∠DFE的度数;
(2)求EC的长.
分析 (1)根据全等三角形对应角相等可得∠D=∠A,∠E=∠B,再利用三角形的内角和等于180°列方程求解即可;
(2)根据全等三角形对应边相等可得BC=EF,然后求出BF=EC,从而得解.
解答 解:(1)∵△ABC≌△DEF,
∴∠D=∠A=30°,∠E=∠B=50°,
∵∠DFE+∠D+∠E=180°,
∴∠DFE=180°-∠D-∠E=180°-30°-50°=100°;
(2)∵△ABC≌△DEF,
∴BC=EF,
∴BC-CF=EF-CF,
即BF=EC,
∵BF=8,
∴EC=8.
点评 本题考查了全等三角形对应角相等,全等三角形对应边相等的性质,三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.下列说法中,不成立的是( )
| A. | 弦的垂直平分线必过圆心 | |
| B. | 弧的中点与圆心的连线垂直平分这条弧所对的弦 | |
| C. | 垂直于弦的直线经过圆心,且平分这条弦所对的弧 | |
| D. | 垂直于弦的直径平分这条弦 |
 如图,设圆形的半径为rm,长方形的长为am、宽为bm.
如图,设圆形的半径为rm,长方形的长为am、宽为bm.