题目内容
2.二元一次方程2x+5y=32的正整数解有( )组.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 把方程用含x的式子表示出y,再根据x、y均为正整数进行讨论即可求得答案.
解答 解:
方程2x+5y=32可变形为y=$\frac{32-2x}{5}$,
∵x、y均为正整数,
∴32-2x>0且为5的倍数,
当x=1时,y=6,
当x=6时,y=4,
当x=11时,y=2,
∴方程2x+5y=32的正整数解有3组,
故选A.
点评 本题主要考查二元一次方程的特殊解,把方程写成用一个未知数表示另一个未知数的形式是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1. 如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
 如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )| A. | 10cm2 | B. | $\frac{10}{n}$cm2 | C. | $\frac{1}{2^n}$cm2 | D. | $10×\frac{1}{2^n}c{m^2}$ |
13. 如图,∠3=∠4,则下列结论一定成立的是( )
如图,∠3=∠4,则下列结论一定成立的是( )
 如图,∠3=∠4,则下列结论一定成立的是( )
如图,∠3=∠4,则下列结论一定成立的是( )| A. | AD∥BC | B. | ∠B=∠D | C. | ∠1=∠2 | D. | ∠B+∠BCD=180° |
17.已知a=$\sqrt{5}$+2,b=2-$\sqrt{5}$,则a2016b2015的值为( )
| A. | -$\sqrt{5}$-2 | B. | -$\sqrt{5}$+2 | C. | 1 | D. | -1 |
14.若关于x、y的方程mx+ny=6的两个解是$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$,则( )
| A. | $\left\{\begin{array}{l}{m=-4}\\{n=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=4}\\{n=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=4}\\{n=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-4}\\{n=3}\end{array}\right.$ |
12.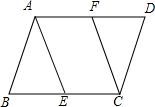 在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
 在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )| A. | AF=CE | B. | AE=CF | C. | ∠BAE=∠FCD | D. | ∠BEA=∠FCE |

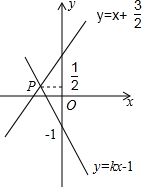 如图,直线y=x+$\frac{3}{2}$与y=kx-1相交于点P,点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集在数轴上表示正确的是( )
如图,直线y=x+$\frac{3}{2}$与y=kx-1相交于点P,点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集在数轴上表示正确的是( )