题目内容
1. 如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )
如图,矩形ABCD的面积为10cm2,它的两条对角线交于,点O1以AB、AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为( )| A. | 10cm2 | B. | $\frac{10}{n}$cm2 | C. | $\frac{1}{2^n}$cm2 | D. | $10×\frac{1}{2^n}c{m^2}$ |
分析 根据矩形的性质对角线互相平分可知O1是AC与DB的中点,根据等底同高得到S△ABO1=$\frac{1}{4}$S矩形,又ABC1O1为平行四边形,根据平行四边形的性质对角线互相平分,得到O1O2=BO2,所以S△ABO2=$\frac{1}{8}$S矩形,…,以此类推得到S△ABO5=$\frac{1}{32}$S矩形,而S△ABO5等于平行四边形ABC5O5的面积的一半,根据矩形的面积即可求出平行四边形ABC5O5和平行四边形ABCnOn的面积.
解答 解:∵设平行四边形ABC1O1的面积为S1,
∴S△ABO1=$\frac{1}{2}$S1,
又∵S△ABO1=$\frac{1}{4}$S矩形,
∴S1=$\frac{1}{2}$S矩形=5=$\frac{5}{{2}^{0}}$;
设ABC2O2为平行四边形为S2,
∴S△ABO2=$\frac{1}{2}$S2,
又∵S△ABO2=$\frac{1}{8}$S矩形,
∴S2=$\frac{1}{4}$S矩形=$\frac{5}{2}$=$\frac{5}{{2}^{1}}$;
,…,
∴平行四边形ABCnOn的面积为$\frac{5}{{2}^{n-1}}$=10×$\frac{1}{{2}^{n}}$(cm2).
故选:D.
点评 此题考查了矩形及平行四边形的性质,要求学生审清题意,找出面积之间的关系,归纳总结出一般性的结论.考查了学生观察、猜想、验证及归纳总结的能力.

练习册系列答案
相关题目
16.甲、乙、丙、丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如表所示( )
则在这四个选手中,成绩最稳定的是( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差 | 0.56 | 0.60 | 0.50 | 0.45 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
2.二元一次方程2x+5y=32的正整数解有( )组.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
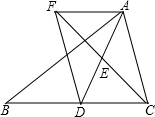 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.



 如图,已知AB=AC=5,BC=3,将BC沿BD所在的直线折叠,使点C落在AB边上的E点处,求三角形AED的周长.
如图,已知AB=AC=5,BC=3,将BC沿BD所在的直线折叠,使点C落在AB边上的E点处,求三角形AED的周长. 知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).
知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).