题目内容
11.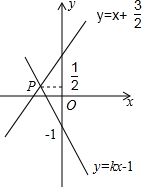 如图,直线y=x+$\frac{3}{2}$与y=kx-1相交于点P,点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集在数轴上表示正确的是( )
如图,直线y=x+$\frac{3}{2}$与y=kx-1相交于点P,点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集在数轴上表示正确的是( )| A. |  | B. |  | C. | 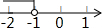 | D. | 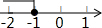 |
分析 先把y=$\frac{1}{2}$代入y=x+$\frac{3}{2}$,得出x=-1,再观察函数图象得到当x>-1时,直线y=x+$\frac{3}{2}$都在直线y=kx-1的上方,即不等式x+$\frac{3}{2}$>kx-1的解集为x>-1,然后用数轴表示解集.
解答 解:把y=$\frac{1}{2}$代入y=x+$\frac{3}{2}$,得
$\frac{1}{2}$=x+$\frac{3}{2}$,解得x=-1.
当x>-1时,x+$\frac{3}{2}$>kx-1,
所以关于x的不等式x+$\frac{3}{2}$>kx-1的解集为x>-1,
用数轴表示为: .
.
故选A.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
2.二元一次方程2x+5y=32的正整数解有( )组.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.下列各组线段中,能组成三角形的是( )
| A. | 2,2,4 | B. | 5,6,12 | C. | 6,9,12 | D. | 5,15,8 |
1.一次函数y=3x-6的图象与x轴的交点坐标是( )
| A. | (0,-6) | B. | (0,6) | C. | (2,0) | D. | (-2,0) |
 知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).
知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).