题目内容
10.已知方程组$\left\{\begin{array}{l}{3x+2y=m+1}\\{2x+y=m-1}\end{array}\right.$,当m=5时,x比y大2.分析 首先将原方程组两个方程相减,得出x+y=2,再与x-y=2联立组成二元一次方程组,然后解得x、y的值,再代入原方程组的任何一个方程即可求出m的值.
解答 解:$\left\{\begin{array}{l}{3x+2y=m+1①}\\{2x+y=m-1②}\end{array}\right.$,
①-②,得x+y=2③,
∵x比y大2,
∴x-y=2④.
③与④组成二元一次方程组$\left\{\begin{array}{l}{x+y=2③}\\{x-y=2④}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$代入②,得4+0=m-1,
解得m=5.
故答案为=5.
点评 本题考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.也考查了解二元一次方程组.

练习册系列答案
相关题目
18. 如图,在△ABC中,∠ACB=90°,D是AB上一点,连接CD,∠ACD=∠B,若BC=13cm,CD=5cm,则BD=( )
如图,在△ABC中,∠ACB=90°,D是AB上一点,连接CD,∠ACD=∠B,若BC=13cm,CD=5cm,则BD=( )
 如图,在△ABC中,∠ACB=90°,D是AB上一点,连接CD,∠ACD=∠B,若BC=13cm,CD=5cm,则BD=( )
如图,在△ABC中,∠ACB=90°,D是AB上一点,连接CD,∠ACD=∠B,若BC=13cm,CD=5cm,则BD=( )| A. | 8cm | B. | 9cm | C. | 10cm | D. | 12cm |
2.二元一次方程2x+5y=32的正整数解有( )组.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
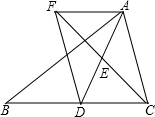 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF. 知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).
知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).