题目内容
12.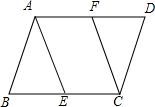 在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )| A. | AF=CE | B. | AE=CF | C. | ∠BAE=∠FCD | D. | ∠BEA=∠FCE |
分析 根据平行四边形的性质和判定即可解决问题.
解答 解:A、错误. ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AF∥EC,
∵AF=EC,
∴四边形AECF是平行四边形.
∴选项A错误.
B、正确.根据AE=CF,所以四边形AECF可能是平行四边形,有可能是等腰梯形,故选项B正确.
C、错误.由∠BAE=∠FCD,∠B=∠D,AB=CD可以推出△ABE≌△CDF,
∴BE=DF,
∵AD=BC,
∴AF=EC,∵AF∥EC,
∴四边形AECF是平行四边形.
故选项C错误.
D、错误.∵∠BEA=∠FCE,
∴AE∥CF,∵AF∥EC,
∴四边形AECF是平行四边形.
故选项D错误.
故选B.
点评 此题考查了平行四边形的性质与判定.解题的关键是选择适宜的证明方法,需要熟练掌握平行四边形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
2.二元一次方程2x+5y=32的正整数解有( )组.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.一次函数y=3x-6的图象与x轴的交点坐标是( )
| A. | (0,-6) | B. | (0,6) | C. | (2,0) | D. | (-2,0) |
2.为了了解某市4万多名初中毕业生的中考数学成绩,任意抽取1000名学生的中考数学成绩进行统计分析,这个问题中,1000是( )
| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
 已知三角形ABC在平面直角坐标系中的位置如图所示.
已知三角形ABC在平面直角坐标系中的位置如图所示.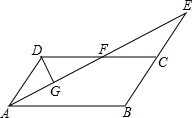 如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.