题目内容
18.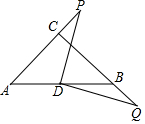 如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.
如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.
分析 DP=DQ成立.连接CD.只要证明△CDP≌△BDQ即可解决问题.
解答 解:DP=DQ成立.
理由: 连接CD.
连接CD.
∵CB=CA,∠ACB=90°,AD=DB,
∴CD=DAD,∠CDB=∠PDQ=90°,∠ACD=∠ABC=45°,
∴∠CDP=∠BDQ,∠DCP=∠DBQ=135°,
在△CDP和△BDQ中,
$\left\{\begin{array}{l}{∠DCP=∠DBQ}\\{CD=DB}\\{∠CDP=∠BDQ}\end{array}\right.$,
∴△CDP≌△BDQ,
∴DP=DQ.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.观察下列各图,图中的小正方形是按一定的规律排列,根据此规律,第10个图中小正方形的个数为( )

| A. | 80 | B. | 81 | C. | 82 | D. | 83 |
6. 如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
 如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )| A. | 110° | B. | 115° | C. | 130° | D. | 135° |
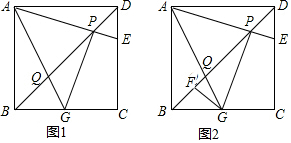
 如图,已知BC∥DE,∠ABC=∠DEF,判断AB和EF的位置关系并说明理由.
如图,已知BC∥DE,∠ABC=∠DEF,判断AB和EF的位置关系并说明理由.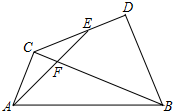 如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,以BC为斜边向外作等腰Rt△DBC,E为CD的中点,AE交BC于F,则EF的长度为$\frac{\sqrt{10}}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,以BC为斜边向外作等腰Rt△DBC,E为CD的中点,AE交BC于F,则EF的长度为$\frac{\sqrt{10}}{3}$. 图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.
图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.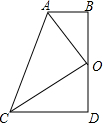 如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,AB+CD=AC.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,AB+CD=AC.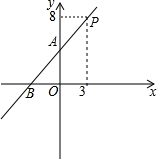 已知:如图,直线y=kx+4(k≠0)经过点P,A,B.
已知:如图,直线y=kx+4(k≠0)经过点P,A,B.