题目内容
9. 图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.
图中,已知AB=12cm,及AC=16cm,M是BC的中点,D点及E点分别在AB和AC之上并且$\frac{AD}{AE}$=$\frac{1}{2}$,求$\frac{DX}{XE}$的值.
分析 连接XC、XB,作XG⊥AB于G,XH⊥AC于H,根据三角形的中线的性质得到△AMB的面积=△AMC的面积,△XMB的面积=△XMC的面积,根据三角形的面积公式计算即可.
解答 解: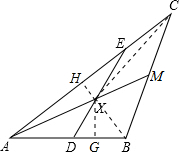 连接XC、XB,作XG⊥AB于G,XH⊥AC于H,
连接XC、XB,作XG⊥AB于G,XH⊥AC于H,
∵M是BC的中点,
∴△AMB的面积=△AMC的面积,△XMB的面积=△XMC的面积,
∴△AXC的面积=△AXB的面积,
∴$\frac{1}{2}$×16×XH=$\frac{1}{2}$×12×XG,
∴$\frac{XH}{XG}$=$\frac{3}{4}$,又$\frac{AD}{AE}$=$\frac{1}{2}$,
∴$\frac{DX}{XE}$=$\frac{\frac{1}{2}×AE×XH}{\frac{1}{2}×AD×XG}$=$\frac{3}{2}$.
点评 本题考查的是平行线分线段成比例定理的应用、三角形的面积公式,灵活运用定理、找准对应关系是解题的关键.

练习册系列答案
相关题目
18. 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
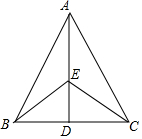 如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由.
如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由.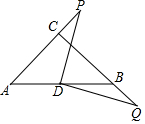 如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.
如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由. 如图,两个45°的三角板叠放在一起,延长BC和AC,分别交DE于点M,N.若∠ABD=30°,则∠AND的大小是30度.
如图,两个45°的三角板叠放在一起,延长BC和AC,分别交DE于点M,N.若∠ABD=30°,则∠AND的大小是30度.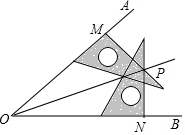 用三角尺可按下面方法画角平分线,在已知的∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?
用三角尺可按下面方法画角平分线,在已知的∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,为什么?