题目内容
9.如图,E是正方形ABCD中CD边上的一点,AE交对角线BD于点P,过点P作AE的垂线交BC于点G,连AG交对角线BD于点Q.(1)求证:AP=PG.
(2)线段BQ、PQ、PD有何数量关系?证明你的结论;
(3)若AB=4,过点G作GF⊥BD于F,直接写出GF+PD=2$\sqrt{2}$.
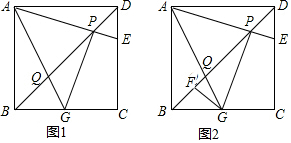
分析 (1)如图1,作辅助线,构建全等三角形,证明△AMP≌△PNG,得AP=PG;
(2)如图2,作BM⊥BD,BM=PD,连AM,依次证明△ADP≌△ABM,△MAQ≌△PAQ,得出△MBQ是直角三角形,根据勾股定理得结论;
(3)如图3,作辅助线,构建全等三角形,先利用勾股定理求BD的长,则可得DH的长,证明△APH≌△PGF,FG=PH,则GF+PD=PD+PH=DH=2$\sqrt{2}$.
解答  证明:(1)如图1,过P作MN⊥AD,交AD于M,交BC于N,
证明:(1)如图1,过P作MN⊥AD,交AD于M,交BC于N,
∵四边形ABCD为正方形,
∴AD∥BC,
∴MN⊥BC,
∴∠AMP=∠GNP=90°,
∴∠PGN+∠GPN=90°,
∵AE⊥PG,
∴∠APG=90°,
∴∠APM+∠GPN=90°,
∴∠PGN=∠APM,
∵BD平分∠ADC,
∴∠ADB=45°,
∴△PMD是等腰直角三角形,
∴PM=DM,
∵AD=CD=MN,
∴AD-DM=MN-PM,
即AM=PN,
∴△AMP≌△PNG,
∴AP=PG;
(2)结论:PQ2=PD2+BQ2.
作BM⊥BD,BM=PD,连AM,MQ,如图2,
∵∠ABD=45°,
∴∠ABM=45°,
∴∠ABM=∠ADB,
∵AB=AD,
∴△ADP≌△ABM(SAS),
∴AM=AP,∠BAM=∠DAP,
由(1)得:AP=PG,
∵AP⊥PG,
∴∠PAQ=45°,
∴∠DAP+∠BAQ=∠BAM+∠BAQ=45°,
即∠MAQ=45°,
易证△MAQ≌△PAQ(SAS),
∴MQ=PQ,
∵∠MBQ=∠MBA+∠ABD=90°,
∴MQ2=BM2+BQ2,
∴PQ2=PD2+BQ2.
(3)如图3,过A作AH⊥BD于H,
∵AB=AD=4,∠BAD=90°,
∴BD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴DH=$\frac{1}{2}$BD=2$\sqrt{2}$,
∵∠AHP=∠GFP=90°,
∴∠HAP+∠APH=90°,
∵∠APH+∠GPF=90°,
∴∠HAP=∠GPF,
∵AP=PG,
∴△APH≌△PGF,
∴FG=PH,
∴GF+PD=PD+PH=DH=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$.
点评 本题是四边形的综合题,考查了正方形的性质、三角形全等的性质和判定、勾股定理、等腰直角三角形的性质,是正方形中常考题型,难度适中,本题的三问证明三角形全等是关键.

 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
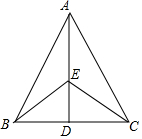 如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由.
如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由.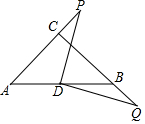 如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.
如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.