题目内容
6. 如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )
如图,AB是半圆O的直径,点C是弧BD的中点,∠ABC=65°,则∠C=( )| A. | 110° | B. | 115° | C. | 130° | D. | 135° |
分析 连接OC,OD,根据等腰三角形的性质可得出∠BCO的度数,再由全等三角形的性质得出△OBC≌△ODC,根据全等三角形的性质即可得出结论.
解答  解:连接OC,OD,
解:连接OC,OD,
∵OC=OB,∠ABC=65°,
∴∠OCB=∠OBC=65°.
∵点C是弧BD的中点,
∴DC=BC.
在△OBC与△ODC中,
∵$\left\{\begin{array}{l}{OB=OD}\\{OC=OC}\\{BC=DC}\end{array}\right.$,
∴△OBC≌△ODC(SSS),
∴∠OCD=∠OCB=65°,
∴∠BCD=∠OCD+∠OCB=65°+65°=130°.
故选C.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,△ABC是等腰三角形,AB=AC.
如图,△ABC是等腰三角形,AB=AC.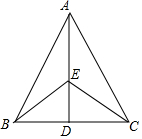 如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由.
如图所示,已知AB=AC,EB=EC,试说明BD=CD的理由. 如图,已知HM平分∠EHD,GB∥HD,∠3=35°.
如图,已知HM平分∠EHD,GB∥HD,∠3=35°.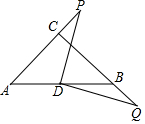 如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.
如图,在△ABC,CB=CA,∠ACB=90°,D为边AB的中点,点P在边AC的延长线上运动,作QD⊥PD,交CB于点Q,则DP=DQ成立吗?请说明理由.