题目内容
6.直线y=$\frac{1}{2}$-$\frac{2}{3}$x经过第一、二、四象限.分析 因为当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,而k=-$\frac{2}{3}$<0,b=$\frac{1}{2}$>0时,由此即可确定直线y=$\frac{1}{2}$-$\frac{2}{3}$x经过的象限.
解答 解:∵k=-$\frac{2}{3}$<0,b=$\frac{1}{2}$>0,
∴直线y=$\frac{1}{2}$-$\frac{2}{3}$x经过第一、二、四象限.
故答案为:一、二、四.
点评 本题考查了一次函数y=kx+b的性质:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小.

练习册系列答案
相关题目
15.下列函数中,y随x增大而减小的是( )
| A. | y=$\frac{2}{x}$ | B. | y=$\frac{-2}{x}$ | C. | y=-2x+4 | D. | y=4+2x |
 如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.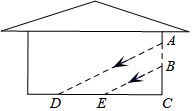 如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.
如图,阳光通过窗口AB照射到室内,在地面上留下4米宽的亮区DE,已知亮区DE到窗口下的墙角距离CE=5米,窗口高AB=2米,那么窗口底边离地面的高BC=2.5 米.