题目内容
9.抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(-1,0)和(3,0),当x<-1时,y随着x的增大而减小.下列给出四个结论::①该抛物线的对称轴是x=1;②abc>0;③a+b>0;④若点A(-2,y1),点B(2,y2)都在抛物线上,则y1<y2.其中结论正确的是①②.(填入正确结论的序号)分析 先依据二次函数的性质确定出抛物线的对称轴和开口方向,然后画出抛物线的大致图象,然后依据函数图形进行判断即可.
解答 解:∵点(-1,0)和(3,0)的纵坐标相同,
∴抛物线的对称轴为x=1,故①正确.
∵抛物线的对称轴为x=1,当x<-1时,y随着x的增大而减小,
∴a>0,-$\frac{b}{2a}$=1.
∴2a+b=0,b<0.
∴a+b=0-a<0,故③错误.
抛物线的大致图象如图所示:
函数图象可知:c<0.
∴abc>0,故②正确.
由函数图象可知y1>0,y2<0,则y1>y2,故④错误.
故答案为:①②.
点评 本题主要考查的是二次函数的图象与系数的关系,熟练掌握二次函数的性质是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
14. 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )| A. | ∠ABC=∠DCB | B. | AC=DB | C. | ∠A=∠D | D. | OC=OB |
 如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)
如图,在⊙O中,∠C=30°,AB=2cm,则弧AB的长等于$\frac{2π}{3}$.(结果保留π)
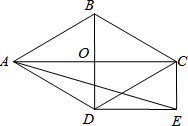 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E. 如图,AB是⊙O的直径,弦AD平分∠BAC,交⊙O于点D,DE⊥AC于点E,求证:DE是⊙O的切线.
如图,AB是⊙O的直径,弦AD平分∠BAC,交⊙O于点D,DE⊥AC于点E,求证:DE是⊙O的切线.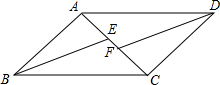 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.