题目内容
19．计算（1）tan45°-（-2）2-|2-$\sqrt{2}$|
（2）（2x-1）2+（x-2）（x+2）-4x（x-$\frac{1}{2}$）
分析 （1）根据特殊角的三角函数值、幂的乘方、绝对值可以解答本题；
（2）根据完全平方公式、平方差公式、单项式乘以多项式可以解答本题．
解答 解：（1）tan45°-（-2）2-|2-$\sqrt{2}$|
=1-4-（2-$\sqrt{2}$）
=1-4-2+$\sqrt{2}$
=-5+$\sqrt{2}$；
（2）（2x-1）2+（x-2）（x+2）-4x（x-$\frac{1}{2}$）
=4x2-4x+1+x2-4-4x2+2x
=x2-2x-3．
点评 本题考查整式的混合运算、实数的运算、特殊角的三角函数值，解题的关键是明确它们各自的计算方法．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
10．
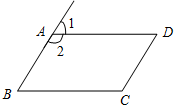如图，四边形ABCD为平行四边形，延长BA，下列各式不一定成立的是（ ）
如图，四边形ABCD为平行四边形，延长BA，下列各式不一定成立的是（ ）| A． | ∠1+∠2=180° | B． | ∠2+∠B=180° | C． | ∠B+∠C=180° | D． | ∠2+∠C=180° |
已知，如图1在Rt△ABC中，∠A=90°，AC=AB=2$\sqrt{2}$，D、E分别是AB、AC的中点，若等腰Rt△ABC绕点A逆时针旋转，得到等腰Rt△AB1C1，设旋转角α（0＜α＜360°），记直线DB1与EC1的交点为P．
已知；如图，在四边形ABCD中，点E、F在AC上，且AE=CF，若四边形EBFD是平行四边形．求证：四边形ABCD是平行四边形．
如图，AB∥CD，E为AC上一点，∠ABE=∠AEB，∠CDE=∠CED．
8．已知在平面直角坐标系中，点A的坐标为（3，0），点B的坐标为（0，4），连接AB，现将线段AB进行平移，平移后得到点B的对应点D的坐标为（1，5），则点A的对应点C的坐标为（ ）
| A． | （3，0） | B． | （4，1） | C． | （2，-1） | D． | （0，5） |
9．某班为奖励在校运动会上取得好成绩的同学，花了200元钱购买甲、乙两种奖品共30件，其中甲种奖品每件8元，乙种奖品每件6元．若设购买甲种奖品x件，乙种奖品y件，则所列方程正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=30}\\{6x+8y=200}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=30}\\{8x+6y=200}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{6x+8y=30}\\{x+y=200}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{8x+6y=30}\\{x+y=200}\end{array}\right.$ |