Question

4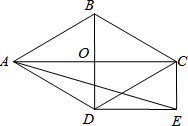．如图，菱形ABCD的对角线AC和BD交于点O，分别过点C、D作CE∥BD，DE∥AC，CE和DE交于点E．
（1）求证：四边形ODEC是矩形；
（2）当∠ADB=60°，AD=2$\sqrt{3}$时，求sin∠AED的值，求∠EAD的正切值．

Answer 1

分析 （1）先证四边形ODEC是平行四边形，然后根据菱形的对角线互相垂直，得到∠DOC=90°，根据矩形的定义即可判定四边形ODEC是矩形；
（2）如图，过点E作EF⊥AD，交AD的延长线于F，构建直角△DEF，在该直角三角形中，∠F=90°，∠EDF=30°，易求DF的长度．所以通过解Rt△AFE来求tan∠EAD的值．

解答 （1）证明：∵CE∥BD，DE∥AC，
∴四边形ODEC是平行四边形．
又∵菱形ABCD，
∴AC⊥BD，
∴∠DOC=90°．
∴四边形ODEC是矩形．

（2）如图，过点E作EF⊥AD，交AD的延长线于F．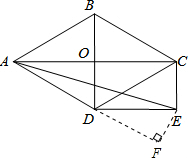
∵AC⊥BD，∠ADB=60°，AD=2$\sqrt{3}$，
∴OD=$\sqrt{3}$，AO=OC=3．
∵四边形ODEC是矩形，
∴DE=OC=3，∠ODE=90°．
又∵∠ADO+∠ODE+∠EDF=180°，
∴∠EDF=30°．
在Rt△DEF中，∠F=90°，∠EDF=30°，
∴EF=$\frac{1}{2}$DE=$\frac{3}{2}$．
∴DF=$\frac{3\sqrt{3}}{2}$．
在Rt△AFE中，∠DFE=90°，
∴tan∠EAD=$\frac{EF}{AF}$=$\frac{EF}{AD+DF}$=$\frac{\frac{3}{2}}{2\sqrt{3}+\frac{3\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{7}$．

点评 本题考查的是矩形的判定与性质，平行四边形的判定和性质，勾股定理的应用，能综合运用知识点进行推理是解此题的关键，注意：菱形的对角线互相平分且垂直．