题目内容
14. 如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )
如图:AB=DC,要使△ABC≌△DCB,不能添加的条件是( )| A. | ∠ABC=∠DCB | B. | AC=DB | C. | ∠A=∠D | D. | OC=OB |
分析 依据全等三角形的判定定理解答即可.
解答 解:A、∵AB=DC,∠ABC=∠DCB,BC=BC,∴△ABC≌△DCB,不符合题意;
B、∵AB=DC,AC=DB,BC=BC,∴△ABC≌△DCB,不符合题意;
C、∵∠AOB=∠DOC,∠A=∠D,AB=DC,∴△AOB≌△DOC,∴AO=DO,BO=CO,∴AC=DB,∵BC=BC,AB=DC,AC=DC,∴△ABC≌△DCB,不符合题意;
D、∵OC=OB,∴∠OCB=∠OBC,∵AB=DC,BC=BC,∠OCB=∠OBC,两边及其一边的对角相等,∴两三角形不一定全等,符合题意.
故选:D.
点评 本题主要考查的是全等三角形的判定,掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
2.当a=-1时,分式$\frac{{{a^2}+a}}{{{a^2}-a}}$( )
| A. | 等于零 | B. | 等于1 | C. | 等于-1 | D. | 没有意义 |
19.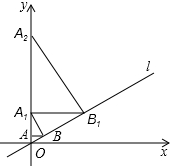 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )| A. | ($\sqrt{3}$×4n,4n) | B. | ($\sqrt{3}$×4n-1,4n-1) | C. | ($\sqrt{3}$×4n-1,4n) | D. | ($\sqrt{3}$×4n,4n-1) |
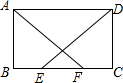 如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.
如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE. 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.