��Ŀ����
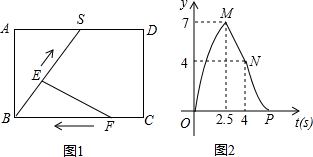
17����ͼ1��S�Ǿ���ABCD��AD����һ�㣬��E��ÿ��kcm���ٶ�������BS-SD-DC�����˶���ͬʱ��F�ӵ�C�����㣬��ÿ��1cm���ٶ��ر�CB�����˶����ҵ�F�˶�����Bʱ��EҲ�˶�����C������E��Fͬʱֹͣ�˶������E��F����t��ʱ����EBF�����Ϊycm2����֪y��t�ĺ���ͼ����ͼ2��ʾ����������OM��NPΪ���������ߣ�MNΪ�߶Σ�������˵�����ٵ�E�˶�����Sʱ������2.5�룬�˶�����Dʱ������4��
�ھ���ABCD�����ڱ߳�ΪBC=6cm��CD=4cm��
��sin��ABS=$\frac{\sqrt{3}}{2}$��
�ܵ�E���˶��ٶ�Ϊÿ��2cm��������ȷ���ǣ�������
| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �ڢۢ� |
���� ����ȷ������ͼ���жϣ�
����ȷ����AB=CD=acm��BC=AD=bcm���г������鼴�ɽ�����⣮
�۴�����BS=2.5k��SD=1.5k����$\frac{BS}{SD}$=$\frac{5}{3}$����SD=3x��BS=5x����RT��ABS�У���AB2+AS2=BS2�г��������x�������жϣ�
����ȷ�����BS���ɽ�����⣮
��� �⣺��ͼ���֪��E�˶�����Sʱ����2.5�룬�˶�����Dʱ������4�룮�ʢ���ȷ��
��AB=CD=acm��BC=AD=bcm��
�����⣬$\left\{\begin{array}{l}{\frac{1}{2}•a•��b-2.5��=7}\\{\frac{1}{2}•a��b-4��=4}\end{array}\right.$
���$\left\{\begin{array}{l}{a=4}\\{b=6}\end{array}\right.$��
����AB=CD=4cm��BC=AD=6cm���ʢ���ȷ��
��BS=2.5k��SD=1.5k��
��$\frac{BS}{SD}$=$\frac{5}{3}$����SD=3x��BS=5x��
��RT��ABS����AB2+AS2=BS2��
��42+��6-3x��2=��5x��2��
���x=1��-$\frac{13}{4}$���ᣩ��
��BS=5��SD=3��AS=3��
��sin��ABS=$\frac{AS}{BS}$=$\frac{3}{5}$�ʢ۴���
��BS=5��
��5=2.5k��
��k=2cm/s���ʢ���ȷ��
��ѡC��
���� ���⿼����κ����ۺ��⡢������Ǻ��������ɶ��������������������ͼ�������֪ʶ������ͼ����Ϣ�ǽ������Ĺؼ���ѧ����δ֪���з����������⣬������ת��Ϊ����ȥ˼���������ν�ϵĺ���Ŀ�������п�ѡ�����е�ѹ���⣮

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�| �ֻ��ͺ� | A�� | B�� | C�� |
| ���ۣ���λ��Ԫ/���� | 900 | 1200 | 1100 |
| Ԥ�ۼۣ���λ��Ԫ/���� | 1200 | 1600 | 1300 |
��2�����y��x֮��ĺ�����ϵʽ��
��3�������������ֻ�ȫ���۳����ۺϿ��Ǹ������أ����ֻ��������ڹ��������ֻ�������������֧�����ַ��ù�1500Ԫ��
�����Ԥ������P��Ԫ����x�������ĺ�����ϵʽ��
��ע��Ԥ������P=Ԥ���ܶ�-������-���ַ��ã�
�����Ԥ����������ֵ����д����ʱ���������ֻ������ٲ���
| A�� | ������ | B�� | ����1 | C�� | ����-1 | D�� | û������ |
 ��ͼ1��ʾ����һ��������ֽ������DEF=25�㣬��ֽ����EF�۵���ͼ2����ͼ2�еġ�BGE�Ķ�����50�㣮
��ͼ1��ʾ����һ��������ֽ������DEF=25�㣬��ֽ����EF�۵���ͼ2����ͼ2�еġ�BGE�Ķ�����50�㣮 ��ͼ����?ABCD�У�E��FΪ��BC�����㣬��BE=CF��AF=DE��
��ͼ����?ABCD�У�E��FΪ��BC�����㣬��BE=CF��AF=DE�� ��ͼ��PA��PB�ֱ����O������A��B���㣬����C=65�㣬���P�Ķ���Ϊ50�㣮
��ͼ��PA��PB�ֱ����O������A��B���㣬����C=65�㣬���P�Ķ���Ϊ50�㣮 ��֪����ͼ1��Rt��ABC�У���A=90�㣬AC=AB=2$\sqrt{2}$��D��E�ֱ���AB��AC���е㣬������Rt��ABC�Ƶ�A��ʱ����ת���õ�����Rt��AB1C1������ת�Ǧ���0������360�㣩����ֱ��DB1��EC1�Ľ���ΪP��
��֪����ͼ1��Rt��ABC�У���A=90�㣬AC=AB=2$\sqrt{2}$��D��E�ֱ���AB��AC���е㣬������Rt��ABC�Ƶ�A��ʱ����ת���õ�����Rt��AB1C1������ת�Ǧ���0������360�㣩����ֱ��DB1��EC1�Ľ���ΪP��