题目内容
18.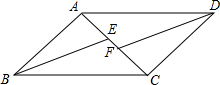 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.(1)求证:AE=CF;
(2)连结ED、FB,判断四边形BEDF是否是平行四边形,说明理由.
分析 (1)根据角平分线的性质先得出∠BEC=∠DFA,然后再证∠ACB=∠CAD,再证出△ABE≌△CDF,从而得出AE=CF;
(2)连接BD交AC于O,则可知OB=OD,OA=OC,又AE=CF,所以OE=OF,然后依据对角线互相平分的四边形是平行四边形即可证明.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠ABC=∠CDA,AB∥CD∴∠BAC=∠DCA,
∵BE、DF分别是∠ABC、∠ADC的平分线,
∴∠ABE=$\frac{1}{2}$∠ABC,∠CDF=$\frac{1}{2}$∠ADC
∴∠ABE=∠CDF,
∴△ABE≌△CDF (ASA),
∴AE=CF;
(2)是平行四边形;
连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO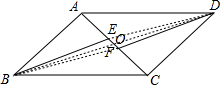
∵AE=CF,
∴AO-AE=CO-CF.
即EO=FO.
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形).
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,解答本题的关键寻找两条线段所在的三角形,然后证明两三角形全等.

练习册系列答案
相关题目
8.一个手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部、B型手机y部,三款手机的进价和预售价如表:
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
10.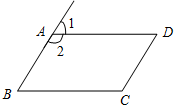 如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
 如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )
如图,四边形ABCD为平行四边形,延长BA,下列各式不一定成立的是( )| A. | ∠1+∠2=180° | B. | ∠2+∠B=180° | C. | ∠B+∠C=180° | D. | ∠2+∠C=180° |
8.已知在平面直角坐标系中,点A的坐标为(3,0),点B的坐标为(0,4),连接AB,现将线段AB进行平移,平移后得到点B的对应点D的坐标为(1,5),则点A的对应点C的坐标为( )
| A. | (3,0) | B. | (4,1) | C. | (2,-1) | D. | (0,5) |
 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°. 已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4).
已知△ABC的顶点A、B、C的坐标分别是(-3,0)、(-1,2)、(-2,4). 已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P.
已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P.