题目内容
11. 如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.
如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.(1)若D是AB上的定点,以BD为直径的⊙O恰好切于AC于E,求⊙O的半径;
(3)若⊙O的圆心是AB上的动点,求⊙O的半径r在怎样的取值范围内能使⊙O与AC相切,且与BC所在直线相交.(第(2)小题直接写答案,不必计算过程)
分析 (1)连接OE,得到OE⊥AC.根据OE∥BC,得到相似三角形,根据相似三角形的对应边的比相等,即可求解;
(2)此题首先可以求得圆和AC,BC相切时,确定r的最小值,再进一步根据BC的长确定r的最大值.
解答  解:(1)如图1,连接OE,得到OE⊥AC.
解:(1)如图1,连接OE,得到OE⊥AC.
则OE∥BC.
∴$\frac{OE}{BC}$=$\frac{OA}{AB}$,即$\frac{r}{6}$=$\frac{10-r}{10}$,
解得:r=$\frac{15}{4}$.
(2)如图2,设⊙O和AC,BC相切于点M,N,连接OM,ON.
设此时圆的半径是r,OB=x.
∵OM∥BC,
∴△AMO∽△ACB,
∴$\frac{OM}{BC}$=$\frac{OA}{AB}$.
即$\frac{r}{6}$=$\frac{10-x}{10}$.
∵ON∥AC,
∴$\frac{ON}{AC}$=$\frac{OB}{AB}$.
即$\frac{r}{8}$=$\frac{x}{10}$,
解得:r=$\frac{24}{7}$.
又∵BC=6,
∴$\frac{24}{7}$<r≤6.
点评 此题考查了切线的性质和相似三角形的判定和性质以及直线与圆的位置关系,熟练应用相似三角形的判定与性质是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
3.若二次函数y=ax2+c(a≠0)的图象上有两点(x1,5),(x2,5),且x1≠x2,则当x取x1+x2时,函数值为( )
| A. | a+c | B. | a-c | C. | -c | D. | c |
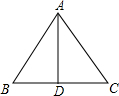 如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为55°.
如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为55°.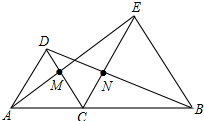 如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证:
如图,A、C、B三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,求证: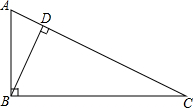 如图,在△ABC中,∠ABC=90°,△ABC∽△BDC,AB=3,AC=5,求DC的长.
如图,在△ABC中,∠ABC=90°,△ABC∽△BDC,AB=3,AC=5,求DC的长.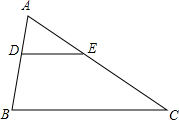 如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长.
如图,点D,E分别在AB,AC上,DE∥BC,若AD:BD=2:3,BC=15cm,求DE的长.