Question

19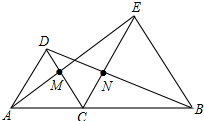．如图，A、C、B三点在同一条直线上，△DAC和△EBC都是等边三角形，AE、BD分别与CD、CE交于点M、N，求证：
①△ACE≌△DCB；
②CM=CN．

Answer 1

分析 （1）根据等边三角形的性质和全等三角形的判定与性质证明即可；
（2）根据全等三角形的判定和性质进行证明即可．

解答 证明：①∵△DAC和△EBC都是等边三角形，
∴AC=CD，CE=BC，∠ACD=∠ECB=60°，
∴∠ACE=∠DCB，
在△ACE与△DCB中，
$\left\{\begin{array}{l}{AC=CD}\\{∠ACE=∠DCB}\\{CE=BC}\end{array}\right.$，
∴△ACE≌△DCB（SAS），
②∵△ACE≌△DCB，
∴∠AEC=∠DBC，
∵∠DCE+∠ACD+∠ECB=180°，∠ACD=∠ECB=60°，
∴∠DCE=∠ECB=60°，
∵CE=BC，∠DCE=∠ECB=60°，∠AEC=∠DBC，
在△EMC与△BNC中，
$\left\{\begin{array}{l}{∠DCE=∠ECB}\\{CE=BC}\\{∠AEC=∠DBC}\end{array}\right.$，
∴△EMC≌△BNC（ASA），
∴CM=CN．

点评 考查了等边三角形的性质及全等三角形的判定方法，关键是根据等边三角形的性质解答．