题目内容
6.分式$\frac{3}{{x}^{2}-2x+1}$、-$\frac{2}{{x}^{2}-1}$、$\frac{1}{{x}^{2}+2x+1}$的最简公分母是(x-1)2(x+1)2.分析 先把各分母因式分解,再根据确定最简公分母的方法求出最简公分母即可.
解答 解:∵$\frac{3}{{x}^{2}-2x+1}$=$\frac{1}{(x-1)^{2}}$,-$\frac{2}{{x}^{2}-1}$=-$\frac{2}{(x+1)(x-1)}$,$\frac{1}{{x}^{2}+2x+1}$=$\frac{1}{(x+1)^{2}}$,
∴最简公分母是(x-1)2(x+1)2;
故答案为:(x-1)2(x+1)2.
点评 此题考查了最简公分母,确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.

练习册系列答案
相关题目
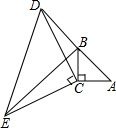 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE. 如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.
如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.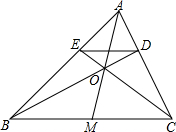 已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC.
已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC.