题目内容
3.若二次函数y=ax2+c(a≠0)的图象上有两点(x1,5),(x2,5),且x1≠x2,则当x取x1+x2时,函数值为( )| A. | a+c | B. | a-c | C. | -c | D. | c |
分析 先找出二次函数y=ax2+c的对称轴是y轴,再找x=0时的函数值即可.
解答 解:二次函数y=ax2+c的对称轴是y轴,当x取x1,x2(x1≠x2)时,函数值相等,即以x1,x2为横坐标的点关于y轴对称,则x1+x2=0,此时函数值为y=ax2+c=0+c=c.
故选D.
点评 本题考查了二次函数图象上点的坐标特征,熟悉二次函数y=ax2+c的对称轴为y轴,两点(x1,5),(x2,5)关于y轴对称是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列各组数据不是勾股数的是( )
| A. | 12,18,22 | B. | 3,4,5 | C. | 7,24,25 | D. | 9,12,15 |
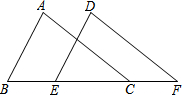 已知:如图AB∥DE,AB=DE,BE=CF,此时AC与DF有什么关系?试说明理由.
已知:如图AB∥DE,AB=DE,BE=CF,此时AC与DF有什么关系?试说明理由. 如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.
如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.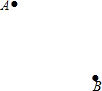 在一次“寻宝”游戏中,寻宝人已经找到了坐标A(3,4)和B(-3,4)两个标志点,并且知道藏宝地点的坐标为C(2,3),除此之外不知道其他信息,如何确定直角坐标系找到“宝藏”?
在一次“寻宝”游戏中,寻宝人已经找到了坐标A(3,4)和B(-3,4)两个标志点,并且知道藏宝地点的坐标为C(2,3),除此之外不知道其他信息,如何确定直角坐标系找到“宝藏”?