题目内容
1.请用一元一次方程解决下面的问题:(1)根据我省“十二五”铁路规划,徐州至连云港的客运专线项目建成后,两地间列车的最短客运时间将由现在的2小时18分钟缩短为36分钟,速每小时将提高260km,求提速后的车速度.(精确到1km/h)
(2)某小组计划做一批“中国结”,如果每人做6个,那么比计划多了8个;如果每人做4个,那么比计划少了42个.请你根据以上信息提出一个用一元一次方程解决的问题,并写出解答过程.
分析 (1)根据路程÷时间=速度,等量关系:提速后的运行速度-原运行的速度=260,列方程求解即可;
(2)可设有x名工人,根据总数相等每人做6个,那么比计划多了8个;如果每人做4个,那么比计划少了42个可列出方程,求解即可.
解答 解:设连云港至徐州客运专线的铁路全长为xkm,
提速前的速度为:$\frac{x}{2\frac{18}{60}}$,提速后的速度为:$\frac{x}{\frac{36}{60}}$,
由题意得,$\frac{x}{\frac{36}{60}}$-$\frac{x}{2\frac{18}{60}}$=260,
解得:x=$\frac{3588}{17}$,
则$\frac{x}{\frac{36}{60}}$≈352km/h.
答:提速后的火车速度约是352km/h;
(2)设计的问题是:该小组有多少名工人?
设有x名工人,根据书的总量相等可得:
6x-8=4x+42,
解得:x=25.
答:这个组有25名工人.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
 如图,已知:∠2=∠3,∠1+∠3=180°,试说明EF∥GH,AB∥CD.
如图,已知:∠2=∠3,∠1+∠3=180°,试说明EF∥GH,AB∥CD. 已知AB是⊙O的一条弦,在圆上找一点C,使得△ABC为等腰三角形.有满足条件的点C共有4个.
已知AB是⊙O的一条弦,在圆上找一点C,使得△ABC为等腰三角形.有满足条件的点C共有4个.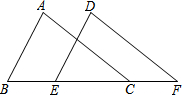 已知:如图AB∥DE,AB=DE,BE=CF,此时AC与DF有什么关系?试说明理由.
已知:如图AB∥DE,AB=DE,BE=CF,此时AC与DF有什么关系?试说明理由. 如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.
如图,已知,在Rt△ABC中,∠C=Rt∠,BC=6,AC=8.