题目内容
19.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等.
分析 (1)根据x轴上点的纵坐标为0列方程求出a,再求解即可;
(2)根据y轴上点的横坐标为0列方程求出a的值,再求解即可;
(3)根据点到x轴、y轴的距离,点的横坐标与纵坐标相等或互为相反数列出方程求出a的值,再求解即可.
解答 解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,
解得a=-4,
所以,a-2=-4-2=-6,
所以,点P(-6,0);
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,
解得a=2,
所以,2a+8=2×2+8=12,
所以,点P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a-2=2a+8或a-2+2a+8=0,
解得a=-10或a=-2,
当a=-10时,a-2=-10-2=-12,
2a+8=2×(-10)+8=-12,
所以,点P(-12,-12),
当a=-2时,a-2=-2-2=-4,
2a+8=2×(-2)+8=4,
点P(-4,4),
综上所述,点P的坐标为(-12,-12)或(-4,4).
点评 本题考查了点的坐标,熟记坐标轴上点的坐标特征是解题的关键,难点在于(3)分两种情况.

练习册系列答案
相关题目
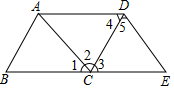 如图,点E在BC的延长线上,下列条件中,
如图,点E在BC的延长线上,下列条件中, 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE. 已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.
已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.