题目内容
14. 如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.
如图,△ABD是等腰直角三角形,点C是BD延长线上一点,F在AC上,AD=AF,E为△ADC内一点,连接AE,BE,AE平分∠CAD,AE⊥BE.(1)若∠EBD=15°,求∠ADF;
(2)求证:BE-AE=DF.
分析 (1)首先求出∠DAF=30°,利用等腰三角形的性质即可解决问题;
(2)作DK∥EF交BE于K.首先证明∠ABO=∠ADE=30°,再证明四边形EFDK是平行四边形,△DEF,△EDK都是等腰直角三角形,由△BDK≌△ADE,推出BK=AD即可解决问题;
解答 (1)解:设AD交BE于O,
∵∠AOE=∠BOD,∠AEO=∠BDO=90°,
∴∠DAE=∠EBD=15°,
∵EA平分∠DAF,
∴∠DAF=30°,
∵AD=AF,
∴∠ADF=∠AFD=75°
(2)证明:作DK∥EF交BE于K.
∵DA=DB,∠ADB=90°,
∴∠ABD=45°,∵∠EBD=15°,
∴∠ABO=30°,∠BOD=∠AOE=75°,
∵∠AEO=∠BDO=90°,
∴△AOE∽△BOD,
∴$\frac{OA}{OB}$=$\frac{OE}{OD}$,
∴$\frac{OA}{OE}$=$\frac{OB}{OD}$,∵∠AOB=∠EOD,
∴△AOB∽△EOD,
∴∠EDO=∠ABO=30°.
即∠ADE=30°,
∵AD=AF.EA平分∠DAF,
∴AE⊥DF,∵AE⊥BE,
∴BE∥DF,
∴四边形EFDK是平行四边形,
∴EF=DK,DF=EK.
∵∠BOD=∠ODE+∠OED=75°,
∴∠ODE=45°,
∴∠EDF=∠ODE=45°,
∵EA=EA,∠EAD=∠EAF,AD=AF,
∴△EAD≌△EAF,
∴ED=EF,
∴∠EDF=∠EFD=45°,
∴△DEF,△EDK都是等腰直角三角形,
∵∠BDA=∠KDE=90°,
∴∠BDK=∠ADE,∵DB=DA,DK=DE,
∴△BDK≌△ADE,
∴BK=AD,
∴BE-BK=EK,
∴BE-AD=DF.
点评 本题科学全等三角形的判定和性质、等腰直角三角形的性质、等腰三角形的性质、平行四边形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
 如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.
如图所示,在△ABC中,AD为BC边上的中线,且AD平分∠BAC,求证:AB=AC.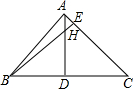 如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由.
如图,AD、BE是△ABC的两条高,AD=BD,H是高AD与BE的交点,试问:BH与AC的长度相等吗?说明你的理由. 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3). 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.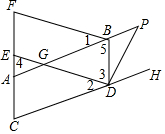 如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.