题目内容
8.(1)计算:$\sqrt{18}$+$\sqrt{12}$-$\sqrt{27}$-$\sqrt{8}$;(2)计算:$\sqrt{1\frac{2}{3}}$+$\sqrt{2}$×$\sqrt{1\frac{1}{5}}$-($\sqrt{3}$+1).
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先进行二次根式的乘法原式,然后把二次根式化为最简二次根式后合并即可.
解答 解:(1)原式=3$\sqrt{2}$+2$\sqrt{3}$-3$\sqrt{3}$-2$\sqrt{2}$
=$\sqrt{2}$-$\sqrt{3}$;
(2)原式=$\frac{\sqrt{15}}{3}$+$\sqrt{2×\frac{6}{5}}$-$\sqrt{3}$-1
=$\frac{\sqrt{15}}{3}$+$\frac{2\sqrt{3}}{5}$-$\sqrt{3}$-1
=$\frac{\sqrt{15}}{5}$-$\frac{3\sqrt{3}}{5}$-1.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
16.在圆面积公式S=πR2中,变量是( )
| A. | S | B. | S与π | C. | S与R2 | D. | S与R |
13.下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.若a,b,c为常数,且(a-c)2>a2+c2,则关于x的一元二次方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一个根或两个不相等的实数根 |
 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.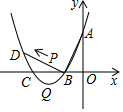 如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.
如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.