题目内容
11. 已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.
已知Rt△ABC,正方形ABGF,正方形ACDE,BAE共线,FD交AE于I,GE交AF于H,求证:AH=AI.
分析 设正方形ABGF,正方形ACDE的边长分别为a、b,先证明△EAH∽△EBG、△FAI∽△FCD,然后依据相似三角形的性质可求得AH=$\frac{ab}{a+b}$、AI=$\frac{ab}{a+b}$,于是可证明AH=AI.
解答 解:设正方形ABGF,正方形ACDE的边长分别为a、b.
∵AH∥BG,
∴△EAH∽△EBG.
∴$\frac{AH}{a}$=$\frac{b}{a+b}$,
∴AH=$\frac{ab}{a+b}$.
∵AI∥CD,
∴△FAI∽△FCD.
∴$\frac{AI}{CD}$=$\frac{AF}{CF}$,
∴$\frac{AI}{b}$=$\frac{a}{a+b}$.
∴AI=$\frac{ab}{a+b}$.
∴AI=AH.
点评 本题主要考查的是相似三角形的性质和判定,熟练掌握相似三角形的性质和判定定理是解题的关键.

练习册系列答案
相关题目
2. 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
16.在圆面积公式S=πR2中,变量是( )
| A. | S | B. | S与π | C. | S与R2 | D. | S与R |
1.已知?ABCD中,∠A+∠C=120°,则∠B的度数是( )
| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
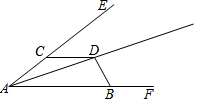 如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC).
如图,D是∠EAF平分线上一点,点C、B分别在射线AE、AF上且CD=BD(AB>AC). 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.